Vetores: Tratamento Algébrico
Plano \(\mathbb{R^2}\)
Um vetor em \(\mathbb{R}^2\) pode ser visualizado geometricamente como uma seta que tem uma direção e uma magnitude (ou comprimento), mas independentemente de onde está posicionado no plano, suas características fundamentais não mudam. A representação algébrica de vetores no plano \(\mathbb{R}^2\) utiliza as componentes \(\mathbf{i}\) e \(\mathbf{j}\), que são, respectivamente, as bases dos eixos \(x\) e \(y\).
Representação:
Um vetor \(\vec{v}\) no \(\mathbb{R}^2\) pode ser expresso em termos de suas componentes ao longo dos eixos \(x\) e \(y\), como:
\(\small \vec{v} = v_x\mathbf{i} + v_y\mathbf{j}\)
Aqui, \(v_x\) e \(v_y\) são escalares que representam, respectivamente, as magnitudes do vetor na direção dos eixos \(x\) e \(y\). Os símbolos \(\mathbf{i}\) e \(\mathbf{j}\) representam os vetores unitários na direção dos eixos \(x\) e \(y\), respectivamente. Um vetor unitário tem uma magnitude de 1 e aponta na direção de um dos eixos do sistema de coordenadas.
\(\mathbb{R^2} = (x,y)\)
onde \((x,y) \in R\)
\(\small (x,y) = (x,0) + (0,y)\)
\(\small (x,y) = x(1,0) + y(0,1)\)
Vetores (base unitário): \(\small \mathbf{i} = (1,0)\) e \(\small \mathbf{j} = (0,1)\)
Logo:
\[\small (x,y) = x\mathbf{i} + y\mathbf{j}\]
Exemplos:
\(\small \vec{v} = 3\mathbf{i} + 4\mathbf{j}\) ou \(\small \vec{v} = (3, 4)\)
\(\small \vec{v} = (-2, 3) = -2\mathbf{i} + 3\mathbf{j}\)
\(\small \vec{v} = (0, 5) = 5\mathbf{j}\)
\(\small \vec{v} = (6, 0) = 6\mathbf{i}\)
Plano \(\mathbb{R^3}\)
Vetores algébricos no espaço tridimensional \(\mathbb{R}^3\), são uma extensão natural dos vetores no plano \(\mathbb{R}^2\), incluindo uma terceira dimensão. Esses vetores são fundamentais para a álgebra linear, física, engenharia, e várias outras ciências e tecnologias que operam em um contexto tridimensional. A representação algébrica desses vetores incorpora uma terceira componente, \(\mathbf{k}\) além das componentes \(\mathbf{i}\) e \(\mathbf{j}\) que representam as direções dos eixos \(x\), \(y\) e \(z\), respectivamente.
Representação:
Um vetor \(\vec{v}\) no \(\mathbb{R}^3\) pode ser expresso em termos de suas componentes ao longo dos eixos \(x\), \(y\) e \(z\), como:
\(\small \vec{v} = v_x\mathbf{i} + v_y\mathbf{j} + v_z\mathbf{k}\)
Aqui, \(v_x\), \(v_y\) e \(v_z\) são escalares que representam, respectivamente, as magnitudes do vetor na direção dos eixos \(x\), \(y\) e \(z\). Os símbolos \(\mathbf{i}\), \(\mathbf{j}\) e \(\mathbf{k}\) representam os vetores unitários nas direções dos respectivos eixos.
\(\mathbb{R^3} = (x,y,z)\)
onde \((x,y,z) \in R\)
\(\small (x,y,z) = (x,0,0) + (0,y,0) + (0,0,z)\)
\(\small (x,y,z) = x(1,0,0) + y(0,1,0) + z(0,0,1)\)
Vetores (base unitário): \(\small \mathbf{i} = (1,0,0)\), \(\small \mathbf{j} = (0,1,0)\) e \(\small \mathbf{k} = (0,0,1)\)
Logo:
\[\small (x,y,z) = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}\]
Exemplos:
\(\small \vec{v} = 2\mathbf{i} + 3\mathbf{j} + 4\mathbf{k}\) ou \(\small \vec{v} = (2,3,4)\)
\(\small \vec{v} = (-1,3,2) = -\mathbf{i} + 3\mathbf{j} + 2\mathbf{k}\)
\(\small \vec{v} = (0,-4,5) = -4\mathbf{j} + 5\mathbf{k}\)
\(\small \vec{v} = (-2,0,1) = -2\mathbf{i} + \mathbf{k}\)
Módulo de um Vetor
A magnitude (ou comprimento) de um vetor \(\vec{v}\) é dada pela raiz quadrada da soma dos quadrados de suas componentes, uma expressão derivada do Teorema de Pitágoras:
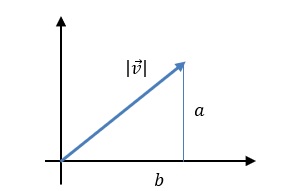
Em \(\mathbb{R}^2\):
\(\small \vec{v} = v_x\mathbf{i} + v_y\mathbf{j} = (v_x,v_y)\)
\(\small |\vec{v}| = \sqrt{v_x^2 + v_y^2}\)
Exemplo:
\(\small \vec{v} = 3\mathbf{i} + 4\mathbf{j}\) ou \(\small \vec{v} = (3, 4)\)
\(\small |\vec{v}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
Em \(\mathbb{R}^3\):
\(\small \vec{v} = v_x\mathbf{i} + v_y\mathbf{j} + v_z\mathbf{k}= (v_x,v_y,v_z)\)
\(\small |\vec{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2}\)
Exemplo:
\(\small \vec{v} = 2\mathbf{i} + 3\mathbf{j} + 4\mathbf{k}\) ou \(\small \vec{v} = (2,3,4)\)
\(\small |\vec{v}| = \sqrt{2^2 + 3^2 + 4^2} = \sqrt{4 + 9 + 16} = \sqrt{29}\)
Vetor Unitário
Para transformar qualquer vetor em um vetor unitário (ou seja, encontrar o vetor unitário na mesma direção de um vetor dado), você divide o vetor pela sua própria magnitude. A fórmula geral para encontrar um vetor unitário \(\hat{u}\) a partir de um vetor \(\vec{v}\) é:
\(\hat{u} = \frac{\vec{u}}{|\vec{u}|}\)
Exemplo:
Em \(\mathbb{R}^2\):
\(\small \vec{v} = 3\mathbf{i} + 4\mathbf{j}\) ou \(\small \vec{v} = (3, 4)\)
\(\small |\vec{v}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
\(\hat{v} = \frac{\vec{v}}{|\vec{v}|} = \frac{\text(3,4)}{5} = \frac{3}{5}\mathbf{i} + \frac{4}{5}\mathbf{j}\)
Em \(\mathbb{R}^3\):
\(\small \vec{v} = v_x\mathbf{i} + v_y\mathbf{j} + v_z\mathbf{k}= (v_x,v_y,v_z)\)
\(\small |\vec{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2}\)
Exemplo:
\(\small \vec{v} = 2\mathbf{i} + 3\mathbf{j} + 4\mathbf{k}\) ou \(\small \vec{v} = (2,3,4)\)
\(\small |\vec{v}| = \sqrt{2^2 + 3^2 + 4^2} = \sqrt{4 + 9 + 16} = \sqrt{29}\)
\(\hat{v} = \frac{\vec{v}}{|\vec{v}|} = \frac{\text(2,3,4)}{\sqrt{29}} = \frac{2}{\sqrt{29}}\mathbf{i} + \frac{3}{\sqrt{29}}\mathbf{j} + \frac{4}{\sqrt{29}}\mathbf{k}\)
Vetor Representado por Dois Pontos
Representar um vetor por meio de dois pontos no espaço é uma forma bastante comum de definir vetores em matemática e física. Vamos considerar dois pontos, \(\small A(x_1, y_1)\) e \(\small B(x_2, y_2)\), em um plano. O vetor \(\small \overrightarrow{AB}\) é definido como o vetor que começa em \(A\) e termina em \(B\). Para encontrar as componentes desse vetor, subtraímos as coordenadas do ponto inicial \(A\) das coordenadas do ponto final \(B\). Assim, as componentes do vetor \(\small \overrightarrow{AB}\) são dadas por:
\(\small \overrightarrow{AB} = (B-A) = (x_2-x_1,y_2-y_1) = (x_2-x_1)\mathbf{i} + (y_2-y_1)\mathbf{j}\)
Exemplo:
\(\small A=(1,2)\) e \(\small B=(4,6)\)
\(\small \overrightarrow{AB} = (B-A) = (4-1,6-2) = 3\mathbf{i} + 4\mathbf{j}\)
Agora, vamos considerar dois pontos, \(A(x_1, y_1, z_1)\) e \(B(x_2, y_2, z_2)\), em um espaço tridimensional. O vetor (\small \overrightarrow{AB}) é definido como o vetor que começa em \(A\) e termina em \(B\). Para encontrar as componentes desse vetor, subtraímos as coordenadas do ponto inicial \(A\) das coordenadas do ponto final \(B\). Assim, as componentes do vetor (\small \overrightarrow{AB}) são dadas por:
\(\small \overrightarrow{AB} = (B-A) = (x_2-x_1,y_2-y_1,z_2-z_1) = (x_2-x_1)\mathbf{i} + (y_2-y_1)\mathbf{j} + (z_2-z_1)\mathbf{k}\)
Exemplo:
\(\small A=(2,-1,3)\) e \(\small B=(5,0,7)\)
\(\small \overrightarrow{AB} = (B-A) = (5-2,0-(-1),7-3) = 3\mathbf{i} + \mathbf{j} + 4\mathbf{k}\)
Distância entre dois Pontos
A ideia de representar um vetor por dois pontos é fundamental em muitas áreas da matemática e da física, pois permite a modelagem de direções e magnitudes no espaço. O vetor não apenas indica a direção do ponto \(A\) para o ponto \(B\), mas sua magnitude (ou comprimento) pode ser calculada usando a fórmula da distância entre dois pontos:
\(\small |\overrightarrow{AB}| = \sqrt{(x_2-x_1)^2 +(y_2-y_1)^2}\)
\(\small \overrightarrow{AB} = 3\mathbf{i} + 4\mathbf{j}\)
\(\small |\overrightarrow{AB}| = \sqrt{3^2 + 4^2} = 5\)
\(\small |\overrightarrow{AB}| = \sqrt{(x_2-x_1)^2 +(y_2-y_1)^2 + (z_2-z_1)^2}\)
\(\small \overrightarrow{AB} = 3\mathbf{i} + \mathbf{j} + 4\mathbf{k}\)
\(\small |\overrightarrow{AB}| = \sqrt{3^2 + 1^2 + 4^2} = \sqrt{26}\)
Operações com Vetores
As operações básicas com vetores em \(\mathbb{R}^2\) e \(\mathbb{R}^3\) incluem soma, subtração, e multiplicação por um escalar:
Soma de Vetores:
Em \(\mathbb{R}^2\):
\(\small \vec{a} = a_x\mathbf{i} + a_y\mathbf{j} = (a_x,a_y)\)
\(\small \vec{b} = b_x\mathbf{i} + b_y\mathbf{j} = (b_x,b_y)\)
\(\small \vec{a} + \vec{b} = (a_x + b_x)\mathbf{j} + (a_y + b_y)\mathbf{j} = (a_x+b_x,a_y+b_y)\)
Exemplo:
\(\small \vec{u} = 2\mathbf{i} + 3\mathbf{j} = (2,3)\)
\(\small \vec{v} = 4\mathbf{i} – \mathbf{j} = (4,-1)\)
\(\small \vec{u} + \vec{v} = 6\mathbf{j} + 2\mathbf{j} = (6,2)\)
Em \(\mathbb{R}^3\):
\(\small \vec{a} = a_x\mathbf{i} + a_y\mathbf{j} + a_z\mathbf{k} = (a_x,a_y,a_z)\)
\(\small \vec{b} = b_x\mathbf{i} + b_y\mathbf{j} + b_z\mathbf{k} = (b_x,b_y,b_z)\)
\(\small \vec{a} + \vec{b} = (a_x + b_x)\mathbf{j} + (a_y + b_y)\mathbf{j} + (a_z + b_z)\mathbf{k} = (a_x+b_x,a_y+b_y,a_z+b_z)\)
Exemplo:
\(\small \vec{u} = 2\mathbf{i} + 2\mathbf{j} + \mathbf{k} = (2,2,1)\)
\(\small \vec{v} = 3\mathbf{i} + \mathbf{j} + 2\mathbf{k} = (3,1,2)\)
\(\small \vec{u} + \vec{v} = 5\mathbf{j} + 3\mathbf{j} + 3\mathbf{k} = (5,3,3)\)
Subtração de Vetores:
Em \(\mathbb{R}^2\):
\(\small \vec{a} = a_x\mathbf{i} + a_y\mathbf{j} = \vec{a} = (a_x,a_y)\)
\(\small \vec{b} = b_x\mathbf{i} + b_y\mathbf{j} = \vec{b} = (b_x,b_y)\)
\(\small \vec{a} – \vec{b} = (a_x – b_x)\mathbf{j} + (a_y – b_y)\mathbf{j} = (a_x-b_x,a_y-b_y)\)
Exemplo:
\(\small \vec{u} = 2\mathbf{i} + 3\mathbf{j} = (2,3)\)
\(\small \vec{v} = 4\mathbf{i} – \mathbf{j} = (4,-1)\)
\(\small \vec{u} – \vec{v} = -2\mathbf{j} + 4\mathbf{j} = (-2,4)\)
Em \(\mathbb{R}^3\):
\(\small \vec{a} = a_x\mathbf{i} + a_y\mathbf{j} + a_z\mathbf{k} = (a_x,a_y,a_z)\)
\(\small \vec{b} = b_x\mathbf{i} + b_y\mathbf{j} + b_z\mathbf{k} = (b_x,b_y,b_z)\)
\(\small \vec{a} – \vec{b} = (a_x – b_x)\mathbf{j} + (a_y – b_y)\mathbf{j} + (a_z – b_z)\mathbf{k} = (a_x-b_x,a_y-b_y,a_z-b_z)\)
Exemplo:
\(\small \vec{u} = 2\mathbf{i} + 2\mathbf{j} + \mathbf{k} = (2,2,1)\)
\(\small \vec{v} = 3\mathbf{i} + \mathbf{j} + 2\mathbf{k} = (3,1,2)\)
\(\small \vec{u} – \vec{v} = -\mathbf{j} + \mathbf{j} -\mathbf{k} = (-1,1,-1)\)
Multiplicação por Escalar:
Em \(\mathbb{R}^2\):
\(\small k\vec{v} = (kv_x)\mathbf{i} + (kv_y)\mathbf{j}\)
Exemplo:
\(\small \vec{v} = 4\mathbf{i} – \mathbf{j} = (4,-1)\)
\(\small 2\vec{v} = 8\mathbf{i} – 2\mathbf{j} = (8,-2)\)
Em \(\mathbb{R}^3\):
\(\small k\vec{v} = (kv_x)\mathbf{i} + (kv_y)\mathbf{j} + (kv_z)\mathbf{k}\)
\(\small \vec{v} = 3\mathbf{i} + \mathbf{j} + 2\mathbf{k} = (3,1,2)\)
\(\small 3\vec{v} = 9\mathbf{i} + 3\mathbf{j} + 6\mathbf{k} = (9,3,6)\)
Além disso, em vetores, temos duas operações especiais:
Produto Escalar: Uma operação que resulta em um escalar, útil para encontrar o ângulo entre vetores ou determinar se dois vetores são perpendiculares.
Produto Vetorial: Uma operação que resulta em um vetor perpendicular aos dois vetores originais.
