Teorema de Pitágoras
O Teorema de Pitágoras é um princípio fundamental da geometria euclidiana que estabelece uma relação específica entre os lados de um triângulo retângulo. Com ele pode-se descobrir a medida de um lado de um triângulo retângulo, a partir da medida de seus outros dois lados.
Definições Básicas:
Triângulo Retângulo: Um triângulo retângulo é um polígono de três lados (triângulo) que possui um ângulo reto (90 graus). Os lados que formam o ângulo reto são chamados de catetos, enquanto o lado oposto ao ângulo reto, o maior dos três lados, é conhecido como hipotenusa.
Teorema de Pitágoras: O teorema afirma que, em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos outros dois lados (os catetos).
\[a^2 = b^2 + c^2\]
onde \(b\) e \(c\) representam os comprimentos dos catetos e \(a\) representa o comprimento da hipotenusa.
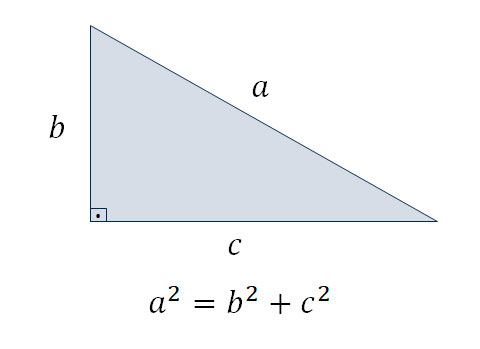
Aplicações
O Teorema de Pitágoras tem varias aplicações tanto dentro quanto fora da matemática. Ele é fundamental na trigonometria, no cálculo de distâncias em geometria analítica, na física, na engenharia e em diversas outras áreas que requerem o cálculo de distâncias ou a verificação de ângulos. Além disso, é utilizado em algoritmos de computação gráfica para determinar distâncias entre pontos em um plano ou espaço.
Exemplos
1. De acordo com triângulo abaixo, encontre o valor de a:
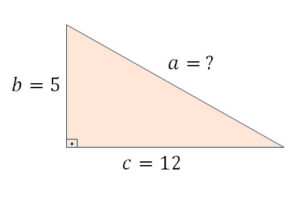
\(\small a^2 = b^2 + c^2\)
\(\small a^2 = 5^2 + 12^2\)
\(\small a = \sqrt{5^2 + 12^2}\)
\(\small a = \sqrt{25 + 144}\)
\(\small a = \sqrt{169}\)
\(\small a = 13\)
2. De acordo com triângulo abaixo, encontre o valor de b:
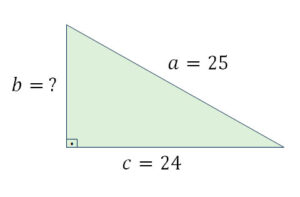
\(\small a^2 = b^2 + c^2\)
\(\small 25^2 = b^2 + 24^2\)
\(\small 625 = b^2 + 576\)
\(\small b^2 = 625 – 576\)
\(\small b^2 = 49\)
\(\small b = \sqrt{49}\)
\(\small b = 7\)
3. De acordo com triângulo abaixo, encontre o valor de c:
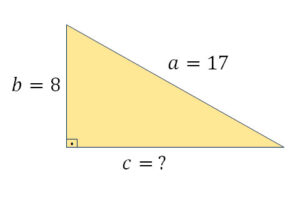
\(\small a^2 = b^2 + c^2\)
\(\small 17^2 = 8^2 + c^2\)
\(\small 289 = 64 + c^2\)
\(\small c^2 = 289 – 64\)
\(\small c^2 = 225\)
\(\small c = \sqrt{225}\)
\(\small c = 15\)
Exercícios
1. Uma escada de 10 metros de comprimento está apoiada contra uma parede vertical. A base da escada está a 6 metros de distância da parede. Qual é a altura alcançada pela escada na parede?
Aproximadamente \(\small 8\) metros
2. Imagine um quadrado cujo lado mede 5 metros. Qual é o comprimento da diagonal do quadrado?
Aproximadamente \(\small 7,07\) metros
