Relações Trigonométricas do Triângulo Retângulo
As relações trigonométricas no triângulo retângulo são fundamentais para a trigonometria, uma área da matemática que estuda as relações entre os ângulos e os lados dos triângulos. No contexto específico do triângulo retângulo, que é um triângulo onde um dos ângulos é reto (90 graus), as relações trigonométricas mais comuns são o seno, cosseno e tangente. Estas relações proporcionam uma forma de relacionar as medidas dos ângulos agudos do triângulo (aqueles menores que 90 graus) com as proporções entre os comprimentos dos seus lados.
Definições das Relações Trigonométricas
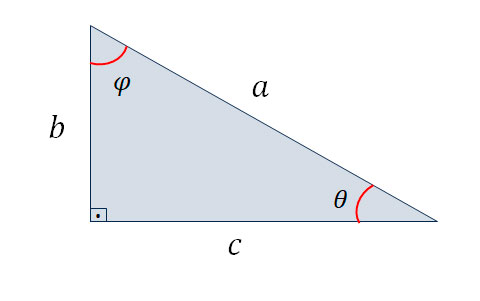
Seno (sen): O seno de um ângulo agudo em um triângulo retângulo é definido como a razão entre o comprimento do cateto oposto a esse ângulo e o comprimento da hipotenusa.
\[sen(\alpha)=\frac{\text{cateto oposto }\alpha}{\text{hipotenusa}}\]
\[sen(\theta)=\frac{b}{a}\]
\[sen(\varphi)=\frac{c}{a}\]
Cosseno (cos): O cosseno de um ângulo agudo em um triângulo retângulo é a razão entre o comprimento do cateto adjacente a esse ângulo e o comprimento da hipotenusa.
\[cos(\alpha)=\frac{\text{cateto adjacente }\alpha}{\text{hipotenusa}}\]
\[cos(\theta)=\frac{c}{a}\]
\[cos(\varphi)=\frac{b}{a}\]
Tangente (tg): A tangente de um ângulo agudo em um triângulo retângulo é definida como a razão entre o comprimento do cateto oposto e o comprimento do cateto adjacente a esse ângulo. Portanto, para um ângulo agudo:
\[tg(\alpha)=\frac{\text{cateto oposto }\alpha}{\text{cateto adjacente }\alpha}\]
\[tg(\theta)=\frac{b}{c}\]
\[tg(\varphi)=\frac{c}{b}\]
Aplicações
As relações trigonométricas são extremamente úteis em diversas áreas, como na engenharia, na física, na arquitetura e até na navegação, pois permitem calcular distâncias inacessíveis e ângulos desconhecidos a partir de informações conhecidas. Por exemplo, conhecendo o seno, cosseno ou tangente de um ângulo e o comprimento de um lado de um triângulo retângulo, é possível determinar os comprimentos dos outros lados.
Exercícios
1. Um farol está localizado a 100 metros de distância de um observador na praia. O ângulo de elevação do topo do farol, a partir do ponto onde o observador está, é de 30 graus. Determine a altura do farol.
\(sin(30°)=\frac{h}{100}\)
Sabendo que \(\sin(30°) = 0,5\), temos:
\(0,5=\frac{h}{100}\)
\(h=50\) metros.
Assim, a altura do farol é de 50 metros.
2. Uma rampa para cadeiras de rodas deve ser construída para superar uma escada de 0,6 metros de altura. Se a norma técnica determina que a inclinação da rampa não deve superar 10 graus para garantir a segurança, qual deve ser o comprimento mínimo da rampa?
\(sin(10°)=\frac{0,6}{L}\)
\(L=\frac{0,6}{sin(10°)}\)
Sabendo que \(\sin(10°) ≈ 0,173648\), temos:
\(L=\frac{0,6}{0,173648}\)
\(L≈3,45\) metros
