Redes Neurais
Redes neurais são um pilar fundamental da inteligência artificial (IA), inspiradas na estrutura e no funcionamento do cérebro humano. Elas são compostas por unidades básicas de processamento, chamadas neurônios artificiais ou perceptron, organizados em camadas. Esses neurônios se conectam uns aos outros e transmitem sinais. A maneira como esses sinais são processados e transferidos entre os neurônios é determinada por pesos, que são ajustados durante o processo de aprendizado da rede.
Estrutura e Funcionamento
A estrutura de uma rede neural típica inclui uma camada de entrada, uma ou mais camadas ocultas e uma camada de saída.
Camada de Entrada: Recebe os dados brutos que serão processados pela rede.
Camadas Ocultas: Realizam a maior parte do processamento por meio de um sistema complexo de pesos e funções de ativação. O número e a complexidade das camadas ocultas podem variar significativamente, dependendo da tarefa em questão.
Camada de Saída: Produz o resultado final do processamento da rede.
Aprendizado
O aprendizado em redes neurais ocorre através de um processo chamado “backpropagation” (retropropagação), durante o qual a rede ajusta seus pesos para minimizar a diferença entre a saída prevista e a saída real. Esse ajuste é feito com base em um conjunto de dados de treinamento, onde a rede é exposta a exemplos que já possuem respostas conhecidas.
Aplicações
As redes neurais são utilizadas em uma ampla gama de aplicações, incluindo:
Reconhecimento de Voz e Imagem: Redes neurais convolucionais (CNNs) são especialmente boas para tarefas que envolvem o processamento de imagens, vídeo e áudio.
Processamento de Linguagem Natural (PLN): Para tradução automática, análise de sentimentos e assistentes virtuais.
Previsões e Análises: Desde a previsão do tempo até a análise de tendências do mercado de ações.
Robótica e Controle Autônomo: Como veículos autônomos e drones.
Perceptron de uma Camada
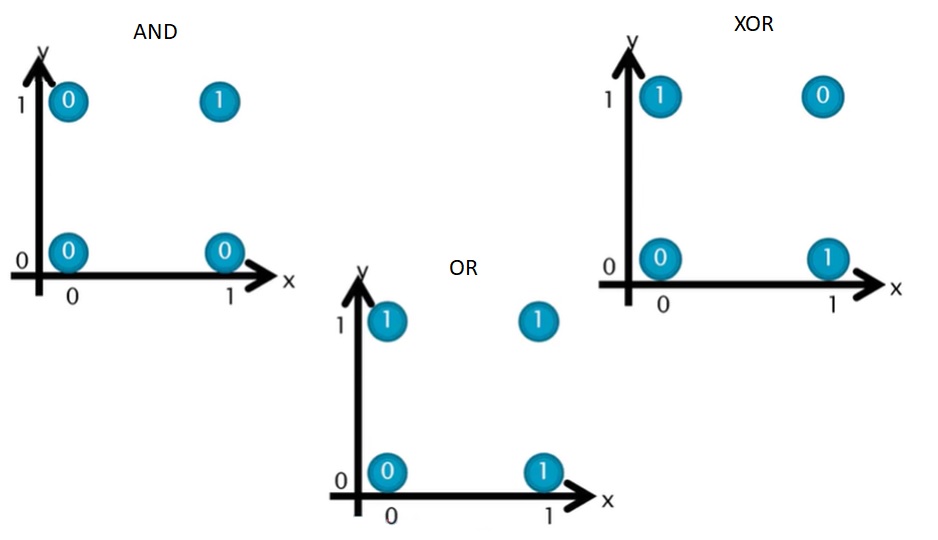
O perceptron de uma camada, também conhecido como perceptron simples ou perceptron de camada única, é um tipo de rede neural artificial que representa a forma mais básica de um neurônio artificial. Foi introduzido por Frank Rosenblatt em 1957 como um modelo para o aprendizado supervisionado de classificadores binários. Um classificador binário é um sistema que pode decidir entre uma de duas possíveis saídas, por exemplo, “sim” ou “não”, “positivo” ou “negativo”.
Estrutura do Perceptron de Uma Camada
A estrutura de um perceptron de uma camada é composta por:
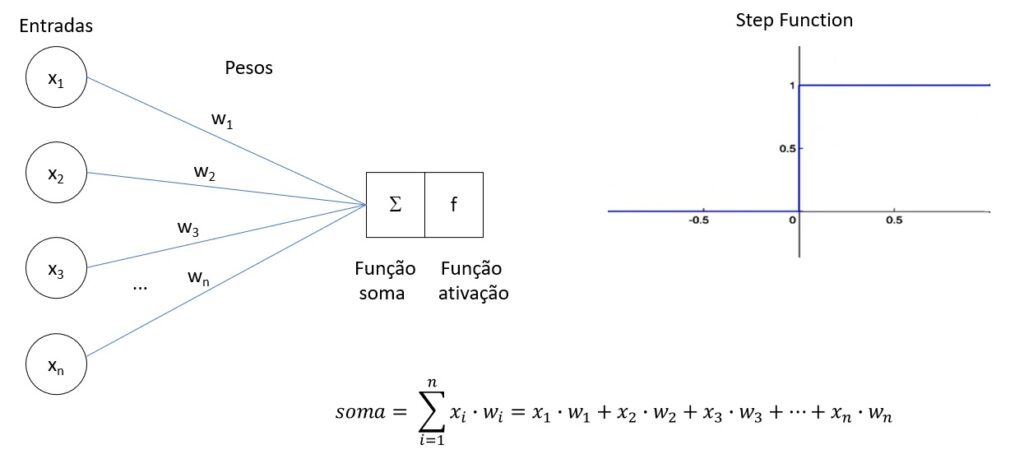
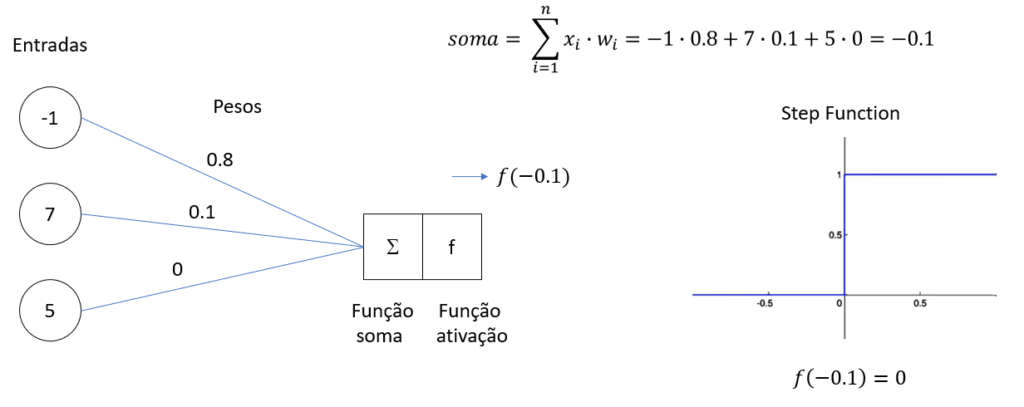
Entradas (x1, x2, …, xn): Cada entrada corresponde a uma característica diferente do dado de entrada. Por exemplo, em um sistema de reconhecimento de padrões, essas entradas poderiam ser os pixels de uma imagem.
Pesos (w1, w2, …, wn): Cada entrada (x_i) é ponderada por um peso (w_i). Esses pesos determinam a importância de cada entrada para a decisão final.
Soma Ponderada: O perceptron calcula uma soma ponderada das entradas e seus respectivos pesos, adicionando também um termo chamado viés (ou bias) (b), que permite ajustar o limiar de ativação do neurônio.
Função de Ativação: A soma ponderada é então passada por uma função de ativação. No caso do perceptron simples, a função de ativação mais comum é a função degrau, que produz uma saída binária (por exemplo, 0 ou 1).
Funcionamento
O processo de funcionamento do perceptron de uma camada segue os seguintes passos:
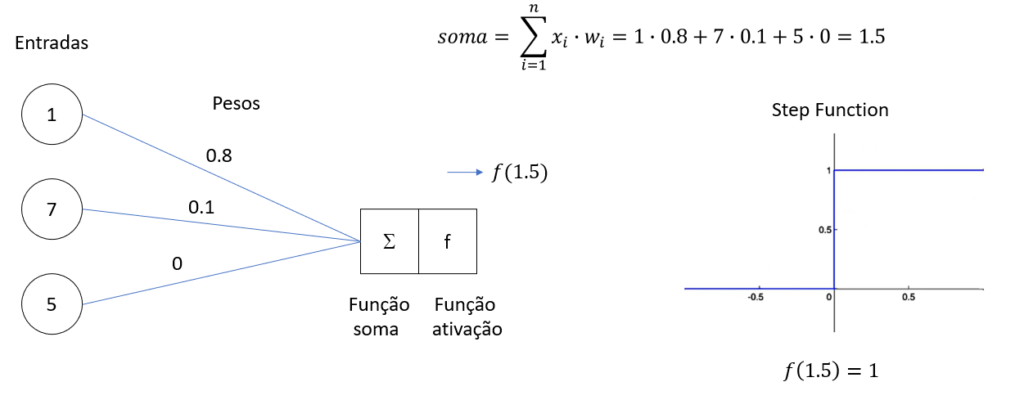
Cálculo da Soma Ponderada: Para um conjunto de entradas (X = (x_1, x_2, …, x_n)) e pesos (W = (w_1, w_2, …, w_n)), o perceptron calcula a soma ponderada (S = w_1x_1 + w_2x_2 + … + w_nx_n + b).
Aplicação da Função de Ativação: A soma ponderada (S) é então aplicada à função de ativação. Se (S) for maior que um certo limiar, o perceptron produzirá a saída 1; caso contrário, produzirá a saída 0.
Ajuste de Pesos: Durante o treinamento, se a saída do perceptron não corresponder à saída esperada, os pesos são ajustados para reduzir o erro. Este processo é repetido várias vezes sobre um conjunto de dados de treinamento até que o perceptron aprenda a classificar corretamente as entradas.
Exemplo:
Pesos
- Pesos são considerados as sinapses
- Peso positivo – sinapse excitadora (aumentando o potencial de ativação do neurônio)
- Peso negativo – sinapse inibidora (diminuindo o potencial de ativação do neurônio)
- Pesos amplificam ou reduzem o sinal de entrada
- Obs: o conhecimento da rede neural são os pesos. A rede neural vai aprender o melhor conjunto de pesos para uma determinada base de dados.
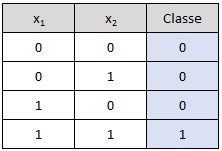
Operador AND:
Erro:
Algoritmo mais simples:
erro = respostaCorreta – respostaCalculada
Os pesos são atualizados até os erros serem pequenos
peso(n+1) = peso(n) + (taxaAprendizagem * entrada * erro)
taxaAprendizagem = 0,1




…
import numpy as np
# Função de ativação: Função Degrau
def step_function(soma):
if (soma >= 1):
return 1
return 0
# Treinamento do Perceptron
def train_perceptron(X, Y, pesos, taxa_aprendizagem, epocas):
for _ in range(epocas):
for i in range(len(X)):
entrada = np.array(X[i])
soma = np.dot(entrada, pesos)
saida = step_function(soma)
erro = abs(Y[i] - saida)
pesos = pesos + taxa_aprendizagem * entrada * erro
return pesos
# Dados de entrada e saída (Tabela-verdade do AND)
entradas = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
saidas = np.array([0, 0, 0, 1])
# Inicialização dos parâmetros
pesos = np.array([0.0, 0.0])
taxa_aprendizagem = 0.1
epocas = 100
# Treinamento
pesos_treinados = train_perceptron(entradas, saidas, pesos, taxa_aprendizagem, epocas)
# Testando o Perceptron após o treinamento
print("Pesos antes do treinamento:", pesos)
print("Pesos após o treinamento:", pesos_treinados)
for entrada in entradas:
soma = np.dot(entrada, pesos_treinados)
saida = step_function(soma)
print("Entrada:", entrada, "Saída:", saida)
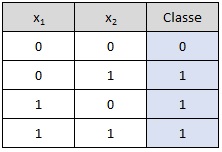
Operador OR:
import numpy as np
# Função de ativação: Função Degrau
def step_function(soma):
if soma >= 1:
return 1
return 0
# Função para treinar o Perceptron
def train_perceptron(X, Y, pesos, taxa_aprendizagem, epocas):
for _ in range(epocas):
for i in range(len(X)):
entrada = np.array(X[i])
soma = np.dot(entrada, pesos)
saida = step_function(soma)
erro = Y[i] - saida
pesos = pesos + taxa_aprendizagem * entrada * erro
return pesos
# Dados de entrada e saída (Tabela-verdade do OR)
entradas = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
saidas = np.array([0, 1, 1, 1])
# Inicialização dos parâmetros
pesos = np.array([0.0, 0.0])
taxa_aprendizagem = 0.1
epocas = 100
# Treinamento
pesos_treinados = train_perceptron(entradas, saidas, pesos, taxa_aprendizagem, epocas)
# Testando o Perceptron após o treinamento
print("Pesos após o treinamento:", pesos_treinados)
for entrada in entradas:
soma = np.dot(entrada, pesos_treinados)
saida = step_function(soma)
print("Entrada:", entrada, "Saída:", saida)
Limitações
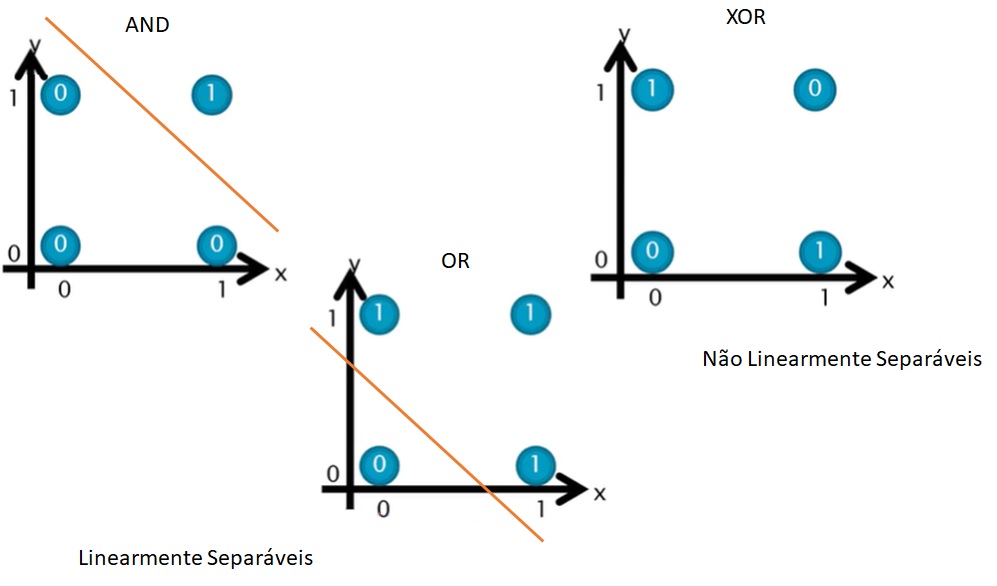
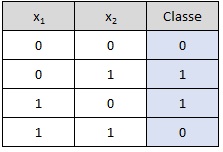
O perceptron de uma camada tem limitações significativas, principalmente sua incapacidade de resolver problemas que não são linearmente separáveis, como o famoso problema do XOR. Isso significa que, se os dados de entrada não puderem ser separados por uma única linha reta (ou hiperplano, em dimensões maiores), o perceptron simples não será capaz de classificá-los corretamente.
Operador XOR:
import numpy as np
# Função de ativação: Função Degrau
def step_function(soma):
if soma >= 1:
return 1
return 0
# Treinamento do Perceptron (Este passo é mais ilustrativo, pois não funcionará para XOR)
def train_perceptron(X, Y, pesos, taxa_aprendizagem, epocas):
for _ in range(epocas):
for i in range(len(X)):
entrada = np.array(X[i])
soma = np.dot(entrada, pesos)
saida = step_function(soma)
erro = Y[i] - saida
pesos = pesos + taxa_aprendizagem * entrada * erro
return pesos
# Dados de entrada e saída (Tabela-verdade do XOR)
entradas = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
saidas = np.array([0, 1, 1, 0])
# Inicialização dos parâmetros
pesos = np.array([0.0, 0.0])
taxa_aprendizagem = 0.1
epocas = 100
# Tentativa de Treinamento (ilustrativa)
pesos_treinados = train_perceptron(entradas, saidas, pesos, taxa_aprendizagem, epocas)
# Testando o Perceptron após o treinamento
print("Pesos após o treinamento (ilustrativo):", pesos_treinados)
for entrada in entradas:
soma = np.dot(entrada, pesos_treinados)
saida = step_function(soma)
print("Entrada:", entrada, "Saída (não será correta para XOR):", saida)
Este código tenta seguir a mesma abordagem de treinamento que seria usada para operadores AND ou OR, mas, como mencionado, não será capaz de aprender corretamente a função XOR devido às limitações do modelo de perceptron de uma camada.
Para implementar corretamente uma rede neural que possa resolver o problema XOR, seria necessário utilizar uma rede com pelo menos uma camada oculta, permitindo que a rede aprenda a separação não linear dos dados. Isso envolveria conceitos mais avançados, como múltiplos neurônios na camada oculta, diferentes funções de ativação (por exemplo, sigmoid), e um algoritmo de otimização mais complexo, como o backpropagation.