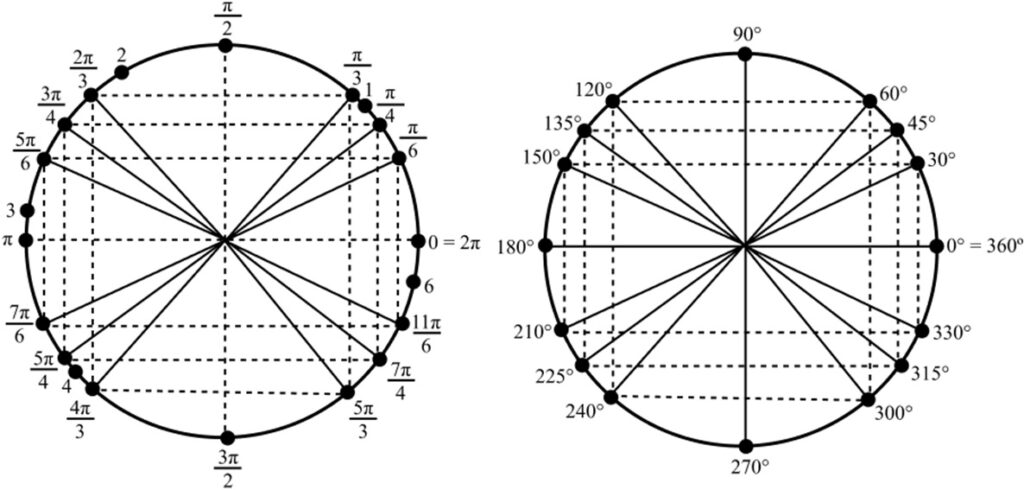
Círculo Trigonométrico
O círculo trigonométrico é uma ferramenta fundamental no estudo da trigonometria, oferecendo uma maneira visual e intuitiva de compreender as relações trigonométricas.
Definição: O círculo trigonométrico é um círculo de raio 1 unidade centrado na origem de um sistema de coordenadas cartesianas.
Pontos Principais: No círculo trigonométrico, os pontos principais correspondem aos ângulos de 0°, 90°, 180°, 270° e 360°, que são equivalentes, em radianos, a \(0\), \(\large \frac{π}{2}\), \(π\), \(\large \frac{3π}{2}\) e \(2π\), respectivamente.
Funções Trigonométricas: As funções seno, cosseno e tangente de um ângulo podem ser representadas no círculo trigonométrico. O seno de um ângulo é a coordenada y do ponto no círculo, o cosseno é a coordenada x, e a tangente é a razão entre o seno e o cosseno desse ângulo.
Quadrantes: O círculo é dividido em quatro quadrantes, cada um representando um intervalo de 90° (ou \(\large \frac{π}{2}\) radianos). As funções trigonométricas têm sinais diferentes em cada quadrante, o que é crucial para resolver problemas trigonométricos.
Identidades Trigonométricas: O círculo trigonométrico ajuda a visualizar e entender várias identidades trigonométricas, como a identidade fundamental da trigonometria \( \sin^2(\theta) + \cos^2(\theta) = 1\)
Período das Funções: O círculo trigonométrico ilustra o conceito de periodicidade das funções trigonométricas. Por exemplo, o seno e o cosseno têm um período de \(2\pi\) radianos, o que significa que seus valores se repetem a cada \(2\pi\) radianos.
Ângulos Negativos e Ângulos Maiores que 360°: No círculo trigonométrico, girar no sentido anti-horário representa um aumento no ângulo, enquanto girar no sentido horário representa um ângulo negativo. Além disso, ângulos maiores que 360° (ou \(2\pi\) radianos) podem ser representados no círculo trigonométrico, continuando a rotação além de um ciclo completo.
Relações com a Geometria Analítica: O círculo trigonométrico estabelece uma conexão entre a trigonometria e a geometria analítica, permitindo a conversão entre coordenadas polares e cartesianas.
Aplicações: Além de seu uso em matemática pura, o círculo trigonométrico tem aplicações práticas em física, engenharia, música e muitas outras áreas, especialmente na análise de fenômenos periódicos.
O círculo trigonométrico não é apenas uma ferramenta para memorizar as funções trigonométricas e suas propriedades, mas também uma maneira de visualizar e entender a relação entre ângulos e razões trigonométricas, facilitando a resolução de problemas complexos em diversas áreas do conhecimento.
Converter Graus para Radianos
Converter graus para radianos é um processo que permite a transição entre duas unidades de medida de ângulos. A conversão se baseia na relação direta entre graus e radianos, onde \(180^\circ\) é equivalente a \(\pi\) radianos. A fórmula para converter graus para radianos é:
\[Radianos = Graus \times \frac{\pi}{180^\circ}\]
Exemplo de Conversão:
Para converter 45 graus para radianos, substituímos o valor na fórmula:
\[45^\circ \times \frac{𝜋}{180^\circ} = \frac{\pi}{4}\]
\(45^\circ = \large \frac{\pi}{4}\) radianos
Função: f(x) = sen(x)
Para calcular o seno \(sen(x)\) dos principais ângulos notáveis entre 0° e 360°, podemos usar o círculo trigonométrico e as propriedades dos ângulos. Os ângulos notáveis comumente considerados são 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, e 330°. Aqui estão os valores de \(sen(x)\) para esses ângulos:
| ÂNGULO (°) | ÂNGULO (RADIANOS) | sen(x) |
|---|---|---|
| \(0^\circ\) | \(0\) | \(0\) |
| \(30^\circ\) | \(\large \frac{\pi}{6}\) | \(\large \frac{1}{2}\) |
| \(45^\circ\) | \(\large \frac{\pi}{4}\) | \(\large \frac{\sqrt{2}}{2}\) |
| \(60^\circ\) | \(\large \frac{\pi}{3}\) | \(\large \frac{\sqrt{3}}{2}\) |
| \(90^\circ\) | \(\large \frac{\pi}{2}\) | \(1\) |
| \(120^\circ\) | \(\large \frac{2\pi}{3}\) | \(\large \frac{\sqrt{3}}{2}\) |
| \(135^\circ\) | \(\large \frac{3\pi}{4}\) | \(\large \frac{\sqrt{2}}{2}\) |
| \(150^\circ\) | \(\large \frac{5\pi}{6}\) | \(\large \frac{1}{2}\) |
| \(180^\circ\) | \(\pi\) | \(0\) |
| \(210^\circ\) | \(\large \frac{7\pi}{6}\) | \(\large -\frac{1}{2}\) |
| \(225^\circ\) | \(\large \frac{5\pi}{4}\) | \(\large -\frac{\sqrt{2}}{2}\) |
| \(240^\circ\) | \(\large \frac{4\pi}{3}\) | \(\large -\frac{\sqrt{3}}{2}\) |
| \(270^\circ\) | \(\large \frac{3\pi}{2}\) | \(-1\) |
| \(300^\circ\) | \(\large \frac{5\pi}{3}\) | \(\large -\frac{\sqrt{3}}{2}\) |
| \(315^\circ\) | \(\large \frac{7\pi}{4}\) | \(\large -\frac{\sqrt{2}}{2}\) |
| \(330^\circ\) | \(\large \frac{11\pi}{6}\) | \(\large -\frac{1}{2}\) |
Função: f(x) = cos(x)
Para calcular o cosseno \(\cos(x)\) dos principais ângulos notáveis entre 0° e 360°, podemos usar o círculo trigonométrico e as propriedades dos ângulos. Os ângulos notáveis comumente considerados são 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, e 330°. Aqui estão os valores de \(\cos(x)\) para esses ângulos:
| ÂNGULO (°) | ÂNGULO (RADIANOS) | COS(x) |
|---|---|---|
| \(0^\circ\) | \(0\) | \(1\) |
| \(30^\circ\) | \(\large \frac{\pi}{6}\) | \(\large \frac{\sqrt{3}}{2}\) |
| \(45^\circ\) | \(\large \frac{\pi}{4}\) | \(\large \frac{\sqrt{2}}{2}\) |
| \(60^\circ\) | \(\large \frac{\pi}{3}\) | \(\large \frac{1}{2}\) |
| \(90^\circ\) | \(\large \frac{\pi}{2}\) | \(0\) |
| \(120^\circ\) | \(\large \frac{2\pi}{3}\) | \(\large -\frac{1}{2}\) |
| \(135^\circ\) | \(\large \frac{3\pi}{4}\) | \(\large -\frac{\sqrt{2}}{2}\) |
| \(150^\circ\) | \(\large \frac{5\pi}{6}\) | \(\large -\frac{\sqrt{3}}{2}\) |
| \(180^\circ\) | \(\pi\) | \(-1\) |
| \(210^\circ\) | \(\large \frac{7\pi}{6}\) | \(\large -\frac{\sqrt{3}}{2}\) |
| \(225^\circ\) | \(\large \frac{5\pi}{4}\) | \(\large -\frac{\sqrt{2}}{2}\) |
| \(240^\circ\) | \(\large \frac{4\pi}{3}\) | \(\large -\frac{1}{2}\) |
| \(270^\circ\) | \(\large \frac{3\pi}{2}\) | \(0\) |
| \(300^\circ\) | \(\large \frac{5\pi}{3}\) | \(\large \frac{1}{2}\) |
| \(315^\circ\) | \(\large \frac{7\pi}{4}\) | \(\large \frac{\sqrt{2}}{2}\) |
| \(330^\circ\) | \(\large \frac{11\pi}{6}\) | \(\large \frac{\sqrt{3}}{2}\) |
Função: f(x) = tg(x)
Para calcular a tangente \(tg(x)\) dos principais ângulos notáveis entre 0° e 360°, utilizamos a relação entre o seno e o cosseno desses ângulos, já que \(tg(x) = \large \frac{sen(x)}{\cos(x)}\). Os ângulos notáveis frequentemente considerados são 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, e 330°. No entanto, é importante lembrar que a tangente não está definida para ângulos nos quais o cosseno é 0, como 90° e 270°, pois isso resultaria em uma divisão por zero.
Abaixo estão os valores de \(tg(x)\) para os ângulos notáveis mencionados, exceto onde a tangente não está definida:
| ÂNGULO (°) | ÂNGULO (RADIANOS) | Tg(X) |
|---|---|---|
| \(0^\circ\) | \(0\) | \(0\) |
| \(30^\circ\) | \(\large \frac{\pi}{6}\) | \(\large \frac{\sqrt{3}}{3}\) |
| \(45^\circ\) | \(\large \frac{\pi}{4}\) | \(1\) |
| \(60^\circ\) | \(\large \frac{\pi}{3}\) | \(\sqrt{3}\) |
| \(90^\circ\) | \(\large \frac{\pi}{2}\) | Não definida |
| \(120^\circ\) | \(\large \frac{2\pi}{3}\) | \(-\sqrt{3}\) |
| \(135^\circ\) | \(\large \frac{3\pi}{4}\) | \(-1\) |
| \(150^\circ\) | \(\large \frac{5\pi}{6}\) | \(\large -\frac{\sqrt{3}}{3}\) |
| \(180^\circ\) | \(\pi\) | \(0\) |
| \(210^\circ\) | \(\large \frac{7\pi}{6}\) | \(\large \frac{\sqrt{3}}{3}\) |
| \(225^\circ\) | \(\large \frac{5\pi}{4}\) | \(1\) |
| \(240^\circ\) | \(\large \frac{4\pi}{3}\) | \(\sqrt{3}\) |
| \(270^\circ\) | \(\large \frac{3\pi}{2}\) | Não definida |
| \(300^\circ\) | \(\large \frac{5\pi}{3}\) | \(-\sqrt{3}\) |
| \(315^\circ\) | \(\large \frac{7\pi}{4}\) | \(-1\) |
| \(330^\circ\) | \(\large \frac{11\pi}{6}\) | \(\large -\frac{\sqrt{3}}{3}\) |