4. Derivadas Parciais de 2a Ordem
Atualizado em: 25 de fevereiro de 2024
Por: Nelson H. Koshoji
4.1. Notações:
Em relação à x:
\[\frac{\partial}{\partial x}(\frac{\partial f}{\partial x}) = \frac{\partial^2 f}{\partial x^2} = f_{xx}\]
Em relação à y:
\[\frac{\partial}{\partial y}(\frac{\partial f}{\partial y}) = \frac{\partial^2 f}{\partial y^2} = f_{yy}\]
Mistas:
\[\frac{\partial}{\partial x}(\frac{\partial f}{\partial y}) = \frac{\partial^2 f}{\partial x\partial y} = f_{xy}\]
\[\frac{\partial}{\partial y}(\frac{\partial f}{\partial x}) = \frac{\partial^2 f}{\partial y\partial x} = f_{yx}\]
Observação: Quando a função z = f(x,y) é contínua no ponto da sua derivação, então:
\[\frac{\partial^2 f}{\partial x\partial y} = \frac{\partial^2 f}{\partial y\partial x}\]
4.2. Esquema:
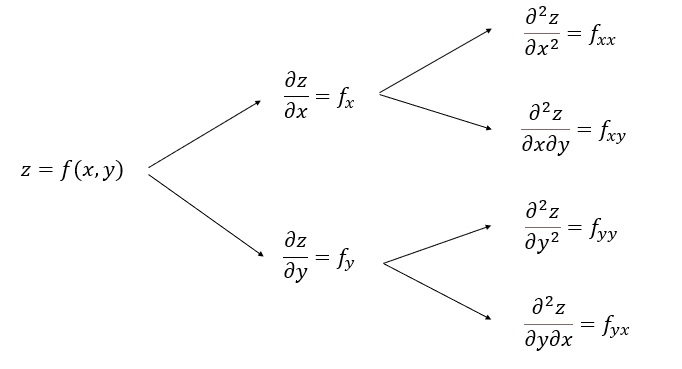
4.3. Exercícios
1. Encontre as Derivadas Parciais das seguintes funções:
a) \(f(x,y) = x^3y^2+x^2y\)
b) \(f(x,y) = xy^3+5xy^2+2x+1\)
c) \(f(x,y) = x^2y-xy^2+2x-y\)
d) \(f(x,y) = xy\)
e) \(f(x,y) = x^2+y^2 – 2x^3y + 5xy^4-1\)
f) \(f(x,y) = x^3y + x^2y^2\)
g) \(f(x,y) = ln(xy)\)
Resposta:
a)
\(\large\frac{\partial^2 f}{\partial x^2} = 6xy^2+2y\)
\(\large\frac{\partial^2 f}{\partial x\partial y} = 6x^2y+2x\)
\(\large\frac{\partial^2 f}{\partial y^2} = 2x^3\)
\(\large\frac{\partial^2 f}{\partial y\partial x} = 6x^2y+2x\)
b)
\(\large\frac{\partial^2 f}{\partial x^2} = 0\)
\(\large\frac{\partial^2 f}{\partial x\partial y} = 3y^2+10y\)
\(\large\frac{\partial^2 f}{\partial y^2} = 6xy+10x\)
\(\large\frac{\partial^2 f}{\partial y\partial x} = 3y^2+10y\)
c)
\(\large\frac{\partial^2 f}{\partial x^2} = 2y\)
\(\large\frac{\partial^2 f}{\partial x\partial y} = 2x-2y\)
\(\large\frac{\partial^2 f}{\partial y^2} = -2x\)
\(\large\frac{\partial^2 f}{\partial y\partial x} = 2x-2y\)
d)
\(\large\frac{\partial^2 f}{\partial x^2} = 0\)
\(\large\frac{\partial^2 f}{\partial x\partial y} = 1\)
\(\large\frac{\partial^2 f}{\partial y^2} = 0\)
\(\large\frac{\partial^2 f}{\partial y\partial x} = 1\)
e)
\(\large\frac{\partial^2 f}{\partial x^2} = 2-12xy\)
\(\large\frac{\partial^2 f}{\partial x\partial y} = -6x^2+20y^3\)
\(\large\frac{\partial^2 f}{\partial y^2} = 2+60xy^2\)
\(\large\frac{\partial^2 f}{\partial y\partial x} = -6x^2+20y^3\)
f)
\(\large\frac{\partial^2 f}{\partial x^2} = 6xy+2y^2\)
\(\large\frac{\partial^2 f}{\partial x\partial y} = 3x^2+4xy\)
\(\large\frac{\partial^2 f}{\partial y^2} = 2x^2\)
\(\large\frac{\partial^2 f}{\partial y\partial x} = 3x^2+4xy\)
g)
\(\large\frac{\partial f}{\partial x} = \frac{1}{x}\)
\(\large\frac{\partial^2 f}{\partial x^2} = -\frac{1}{x^2}\)
\(\large\frac{\partial^2 f}{\partial x\partial y} = 0\)
\(\large\frac{\partial f}{\partial x} = \frac{1}{y}\)
\(\large\frac{\partial^2 f}{\partial y^2} = -\frac{1}{y^2}\)
\(\large\frac{\partial^2 f}{\partial y\partial x} = 0\)
