3. Derivadas Parciais
Atualizado em: 13 de fevereiro de 2024
Por: Nelson H. Koshoji
3.1. Função de Uma Variável e Sua Derivada
Representação: \[y=f(x)\]
Seja a função:
\[f(x) = 2x^3+5x+1\]
ou
\[y = 2x^3+5x+1\]
A sua derivada é representada da seguinte forma:
\[y’ = f'(x) = \frac{dy}{dx} = 6x^2+5\]
3.2. Derivadas de Funções Multivariáveis
Uma função multivariável é uma função que tem mais de uma variável independente. Por exemplo, \(z=f(x, y)\) é uma função de duas variáveis independentes \(x\) e \(y\). No contexto de funções de várias variáveis, surge a necessidade de entender como a função muda em relação a cada uma das suas variáveis, mantendo as outras constantes. Isso nos leva ao conceito de derivada parcial.
A derivada parcial de uma função \(f(x,y)\) em relação à variável \(x\), denotada por \[ \frac{\partial f}{\partial x} = f_x \] … é a taxa de variação da função em relação a \(x\) quando \(y\) é mantida constante.
Analogamente, a derivada parcial de \(f(x,y)\) em relação a \(y\) é \[\frac{\partial f}{\partial y} = f_y \] … que mede a taxa de variação da função em relação a \(y\) enquanto \(x\) é mantido constante.
3.3. Cálculo da Derivada Parcial
Para calcular uma derivada parcial, tratamos todas as outras variáveis exceto a que estamos derivando como constantes e aplicamos as regras de derivação da mesma maneira que faríamos para funções de uma única variável.
Por exemplo, se temos uma função: \[f(x,y) = 16 – 4x^2 – y^2\] … as derivadas parciais seriam:
Em relação a \(x\):
\[\frac{\partial f}{\partial x} = -8x\]
Em relação a \(y\):
\[\frac{\partial f}{\partial y} = -2y\]
Outro exemplo, se temos uma função: \[f(x,y) = x^2 + y^3-3x^3y^2+3^3\] … as derivadas parciais seriam:
Em relação a \(x\):
\[\frac{\partial f}{\partial x} = 2x-9x^2y^2\]
Em relação a \(y\):
\[\frac{\partial f}{\partial y} = 3y^2-6x^3y\]
3.4. Interpretação Geométrica
A interpretação geométrica de uma derivada parcial é a inclinação da tangente à curva que se obtém ao cortar a superfície definida pela função \(f(x,y)\) com um plano paralelo a um dos eixos de coordenadas.
Por exemplo:
Seja: \[f(x,y) = 16 – 4x^2 – y^2\] Encontre a derivada parcial da função quando \(x = 0,5\) e um plano fixo em \(y=2\).
\[\frac{\partial f}{\partial x}\] dá a inclinação da tangente à curva de interseção do plano que mantém \(y\) constante.
\[\frac{\partial f}{\partial x} = -8x\]
Substituindo \(x=0,5\), temos:
\[\frac{\partial f}{\partial x} = -8x = -8(0,5) = -4\]
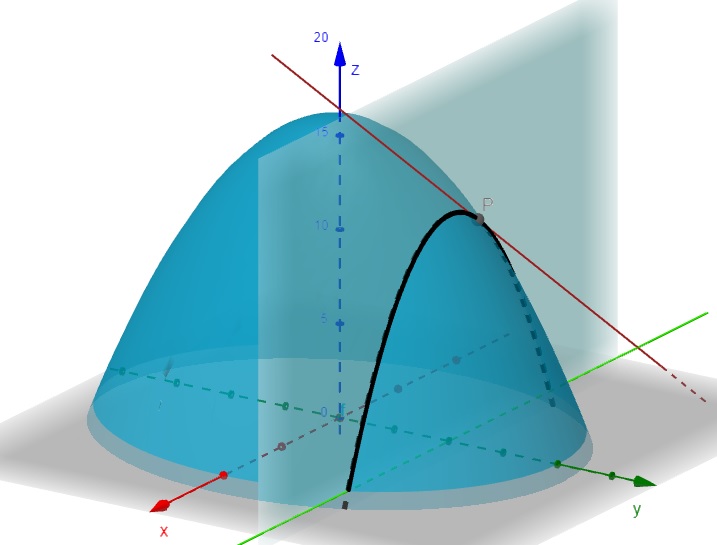
Figura 3.1: Derivada Parcial da Função em relação a x – geogebra.org
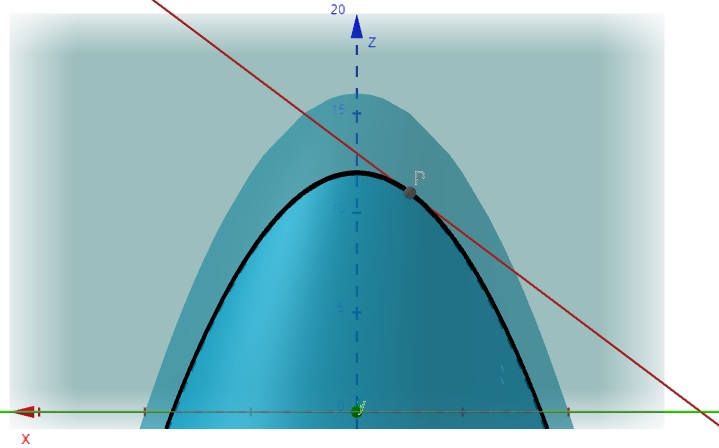
Figura 3.2: Derivada Parcial da Função em relação a x – Vista Frontal – geogebra.org
Se substituir \(x=-0,5\), temos:
\[\frac{\partial f}{\partial x} = -8x = -8(-0,5) = 4\]
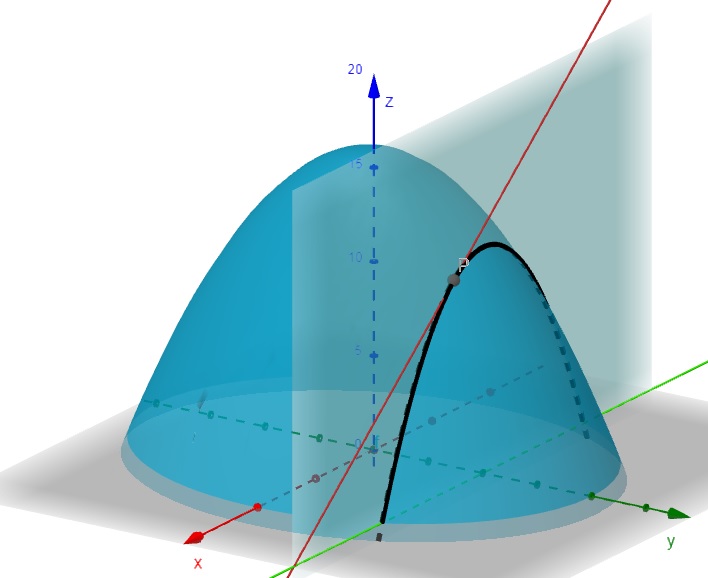
Figura 2.3: Derivada Parcial da Função em relação a x – geogebra.org
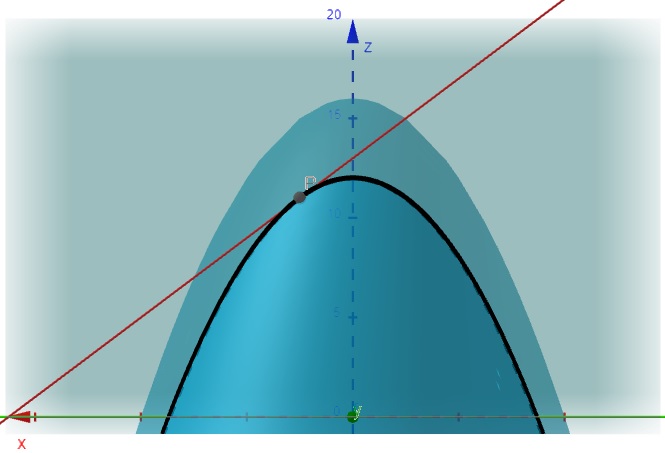
Figura 2.4: Derivada Parcial da Função em relação a x – Vista Frontal – geogebra.org
De forma análoga, seja: \[f(x,y) = 16 – 4x^2 – y^2\]
Encontre a derivada parcial da função quando \(y = 1,5\) e um plano fixo em \(x=1\).
\[\frac{\partial f}{\partial x}\] dá a inclinação da tangente à curva de interseção do plano que mantém \(x\) constante.
\[\frac{\partial f}{\partial x} = -2y\]
Substituindo \(y=1,5\), temos:
\[\frac{\partial f}{\partial x} = -2y = -2(1,5) = -3\]
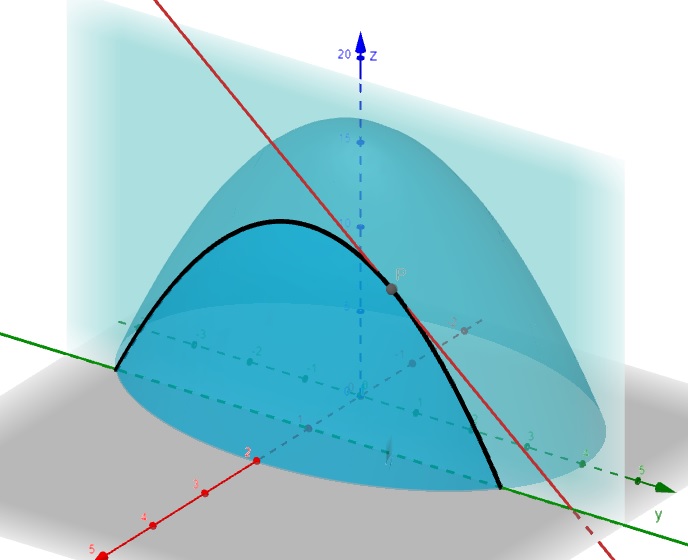
Figura 2.5: Derivada Parcial da Função em relação a y – geogebra.org
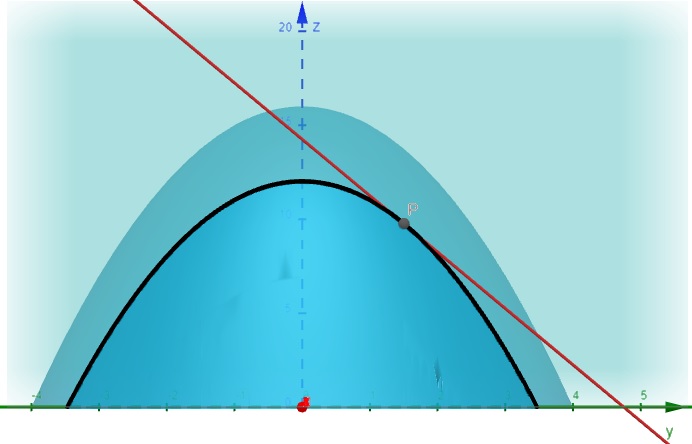
Figura 2.6: Derivada Parcial da Função em relação a y – Vista Frontal – geogebra.org
Se substituir \(y=-1,5\), temos:
\[\frac{\partial f}{\partial x} = -2y = -2(-1,5) = 3\]
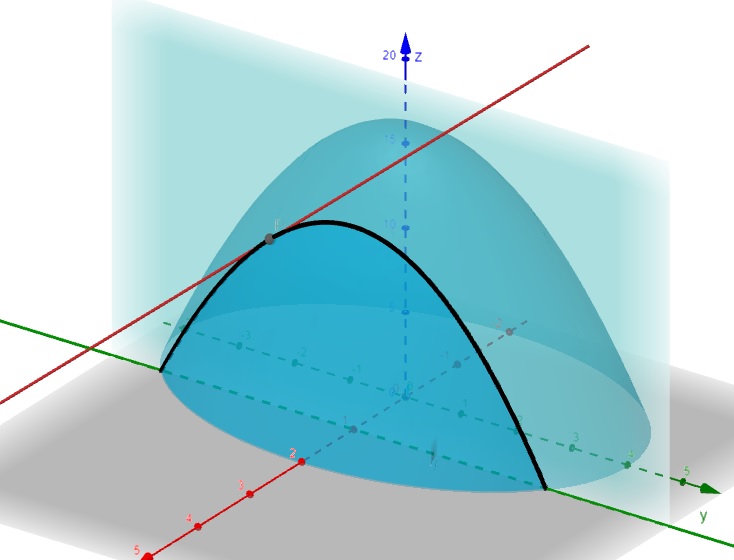
Figura 2.7: Derivada Parcial da Função em relação a y – geogebra.org
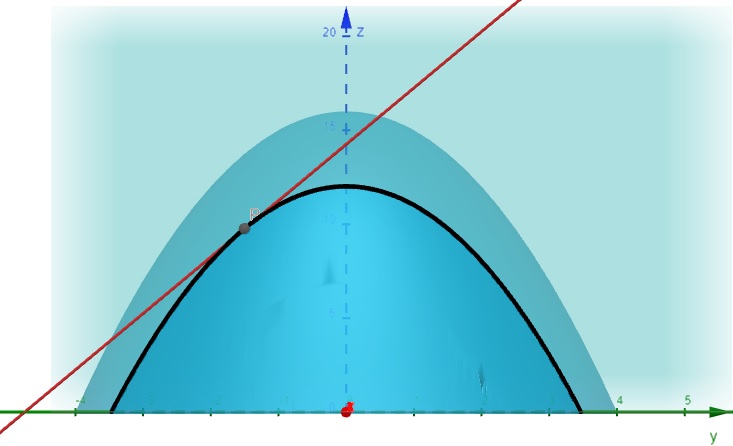
Figura 2.8: Derivada Parcial da Função em relação a y – Vista Frontal – geogebra.org
3.5. Exercícios
1. Seja a função \[f(x,y) = 9 – x^2 – y^2\] … ao fixar y = 1 e fazer a variação de x, encontre a derivada parcial e sua declividade quando x = 1, 2 e 3, respectivamente.
2. De forma análoga, seja a função \[f(x,y) = 9 – x^2 – y^2\] … ao fixar x = 1 e fazer a variação de y, encontre a derivada parcial e sua declividade quando y = 1, 2 e 3, respectivamente.
3. Encontre a declividade da reta tangente a curva abaixo, resultante da intersecção da função f(x,y) com o plano y = 2, no ponto P(2,2,8)
\[f(x,y) = x^2 + y^2\]
4. Encontre a declividade da reta tangente a curva abaixo, resultante da intersecção da função f(x,y) com o plano x = 1, no ponto P(1,1,2)
\[f(x,y) = 4 – x^2 – y^2 \]
5. Encontre a declividade da reta tangente a curva abaixo, resultante da intersecção da função f(x,y) com o plano x = -1, no ponto P(-1,1,-2)
\[f(x,y) = x^2 + y^2 -2x^3y+5xy^4 – 1\]
3.6. Derivadas de Várias Variáveis Independentes
\[w=f(x,y,z)\]
Encontre as derivadas parciais da seguinte função:
\[f(x,y,z) = x^2z+yz^2\]
\(\large\frac{\partial w}{\partial x} = 2xz\)
\(\large\frac{\partial w}{\partial y} = z^2\)
\(\large\frac{\partial w}{\partial z} = x^2 + 2yz\)
Exercício: Encontre as derivadas parciais da seguinte função:
\[f(x,y,z) = x^2z+ye^{3z}\]
Figura 2.9: Curva de Nível – geogebra.org
3.7. Exercícios
1. Encontre as Derivadas Parciais das seguintes funções:
a) \(f(x,y) = xy^2\)
b) \(f(x,y) = 3x^4y^5\)
c) \(f(x,y) = 3x^3y^2\)
d) \(f(x,y) = 6x^2y – 5x^3y^2 – 6y\)
e) \(f(x,y) = 4xy – 2x^2y^2 + 3x^3y^2\)
f) \(f(x,y) = x^5 + 3x^3y^2 + 3xy^4\)
g) \(f(x,y) = 3x^4y^5 + y^2 + 3\)
h) \(f(x,y) = 2x^2y^3 – 3x + 4y\)
i) \(f(x,y) = x^3 + y^3 – 2x + 2y\)
j) \(f(x,y) = 4x^3y^{-2} – 2xy – 3x – 4y – 7\)
k) \(f(x,y) = x^2 + 2xy^2 + \frac{2y}{3x}\)
l) \(f(x,y,z) = x^2yz – xz\)
m) \(f(x,y,z) = \sqrt{x^2+y^2+z^2}\)
n) \(f(x,y) = \sqrt{x^3+y^4+4}\)
o) \(f(x,y) = \ln{(x^2+y^2)}\)
p) \(f(x,y) = e^{x^2y}\)
q) \(f(x,y) = sen{(x^2y)}\)
r) \(f(x,y) = cos{(5x-3y)}\)
Resposta:
a)
\(\large\frac{\partial f}{\partial x} = y^2\)
\(\large\frac{\partial f}{\partial y} = 2xy\)
b)
\(\large\frac{\partial f}{\partial x} = 12x^3y^5\)
\(\large\frac{\partial f}{\partial y} = 15x^4y^4\)
c)
\(\large\frac{\partial f}{\partial x} = 9^2y^2\)
\(\large\frac{\partial f}{\partial y} = 6x^3y\)
d)
\(\large\frac{\partial f}{\partial x} = 12xy-15x^2y^2\)
\(\large\frac{\partial f}{\partial y} = 6x^2-10x^3y-6\)
e)
\(\large\frac{\partial f}{\partial x} = 4y-4xy^2+9x^2y^2\)
\(\large\frac{\partial f}{\partial y} = 4x-4x^2y+6x^3y\)
f)
\(\large\frac{\partial f}{\partial x} = 5x^4+9x^2y^2+3y^4\)
\(\large\frac{\partial f}{\partial y} = 6x^3y+12xy^3\)
g)
\(\large\frac{\partial f}{\partial x} = 12x^3y^5\)
\(\large\frac{\partial f}{\partial y} = 15x^4y^4+2y\)
h)
\(\large\frac{\partial f}{\partial x} = 4xy^3-3\)
\(\large\frac{\partial f}{\partial y} = 6x^2y^2+4\)
i)
\(\large\frac{\partial f}{\partial x} = 3x^2-2\)
\(\large\frac{\partial f}{\partial y} = 3y^2+2\)
j)
\(\large\frac{\partial f}{\partial x} = \frac{12x^2}{y^2}-2y-3\)
\(\large\frac{\partial f}{\partial y} = -\frac{8x^3}{y^3}-2x-4\)
k)
\(\large\frac{\partial f}{\partial x} = 2x+2y^2-\frac{2y}{3x^2}\)
\(\large\frac{\partial f}{\partial y} = 4xy+\frac{2}{3x}\)
l)
\(\large\frac{\partial f}{\partial x} = 2xyz-z\)
\(\large\frac{\partial f}{\partial y} = x^2z\)
\(\large\frac{\partial f}{\partial z} = x^2y-x\)
m)
\(\large\frac{\partial f}{\partial x} = \frac{x}{\sqrt{x^2+y^2+z^2}}\)
\(\large\frac{\partial f}{\partial y} = \frac{y}{\sqrt{x^2+y^2+z^2}}\)
\(\large\frac{\partial f}{\partial z} = \frac{z}{\sqrt{x^2+y^2+z^2}}\)
m)
\(\large\frac{\partial f}{\partial x} = \frac{3x^2}{2\sqrt{x^3+y^4+4}}\)
\(\large\frac{\partial f}{\partial y} = \frac{2y^3}{\sqrt{x^3+y^4+4}}\)
o)
\(\large\frac{\partial f}{\partial x} = \frac{2x}{x^2+y^2}\)
\(\large\frac{\partial f}{\partial y} = \frac{2y}{x^2+y^2}\)
p)
\(\large\frac{\partial f}{\partial x} = 2xy \cdot e^{x^2y}\)
\(\large\frac{\partial f}{\partial y} = x^2 \cdot e^{x^2y}\)
q)
\(\large\frac{\partial f}{\partial x} = 2xy \cdot cos{(x^2y)}\)
\(\large\frac{\partial f}{\partial y} = x^2 \cdot cos{(x^2y)}\)
r)
\(\large\frac{\partial f}{\partial x} = -5 \cdot sen{(5x-3y)}\)
\(\large\frac{\partial f}{\partial y} = 3 \cdot sen{(5x-3y)}\)
