2. Funções Multivariáveis
Atualizado em: 12 de fevereiro de 2024
Por: Nelson H. Koshoji
2.1. Introdução
Funções multivariáveis, também conhecidas como funções de várias variáveis, são funções que dependem de mais de uma variável independente. Em outras palavras, enquanto uma função univariada tem a forma \(f(x)\), onde \(x\) é a única variável independente, uma função multivariável pode ter a forma \(f(x, y, …, z)\), onde \(x, y, …, z\) representam as variáveis independentes.
Essas funções são extremamente úteis em diversas áreas da matemática, física, engenharia, economia, e muitas outras ciências, pois muitos fenômenos e problemas reais dependem de mais de uma variável para serem descritos adequadamente. Por exemplo, a temperatura em um ponto específico do espaço pode ser uma função de sua localização em três dimensões espaciais (latitude, longitude, altitude) e do tempo, tornando-se uma função multivariável \(T(x, y, z, t)\).
2.2. Principais Características
Domínio: O domínio de uma função multivariável é um conjunto de n-tuplas (pares, trios, etc.) de números que representam as entradas possíveis para a função. Por exemplo, o domínio de uma função de duas variáveis \(f(x, y)\) pode ser uma região específica do plano \(xy\).
Gráfico: O gráfico de uma função de duas variáveis, \(f(x, y)\), é uma superfície no espaço tridimensional. A representação gráfica de funções que dependem de mais de duas variáveis não pode ser facilmente visualizada no espaço tridimensional.
Curvas de Nível: Para funções de duas variáveis, uma forma útil de representação é através das curvas de nível (ou linhas de contorno), que são gráficos bidimensionais mostrando os locais onde a função tem o mesmo valor.
Derivação e Integração: As técnicas de cálculo para funções multivariáveis incluem derivação e integração parciais, onde derivadas e integrais são calculadas em relação a uma das variáveis, mantendo as outras constantes.
2.3. Alguns Exemplos de Funções Multivariadas
Função de Duas Variáveis:
a) Superfície Parabolóide: \[f(x, y) = x^2 + y^2\].
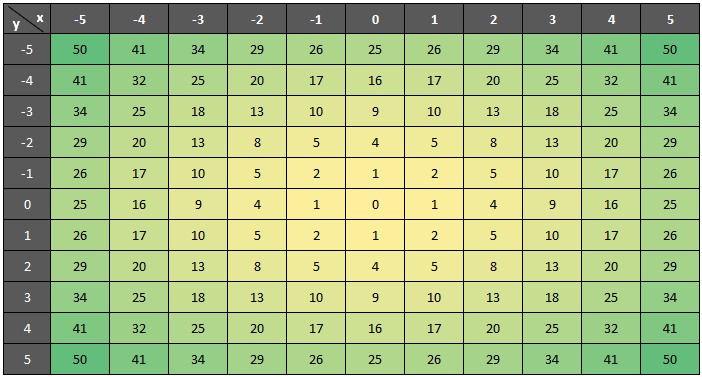
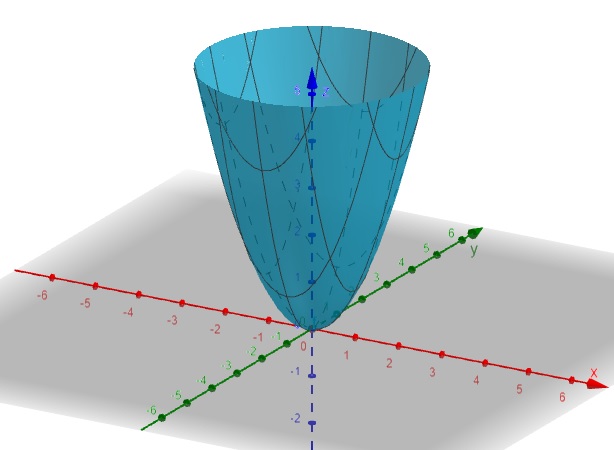
Figura 2.1: Superfície Parabolóide – geogebra.org
b) Superfície Cônica: \[f(x, y) = \sqrt{x^2+y^2}\]
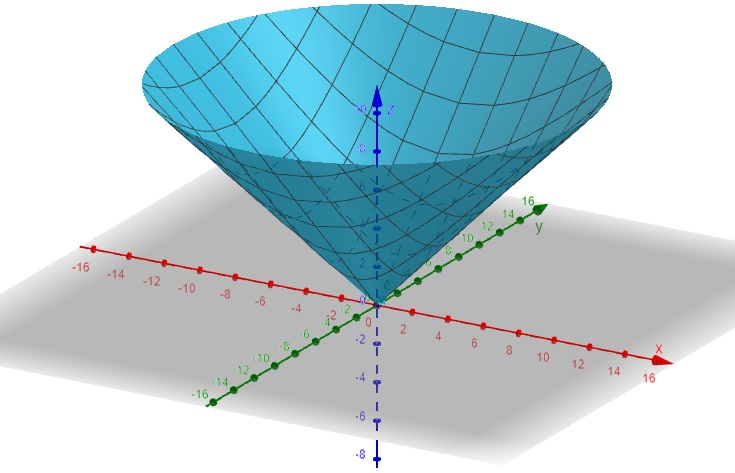
Figura 2.2: Superfície Cônica – geogebra.org
c) Superfície Elipsóide: \[f(x, y) = \sqrt{25-(x^2+y^2)}\]
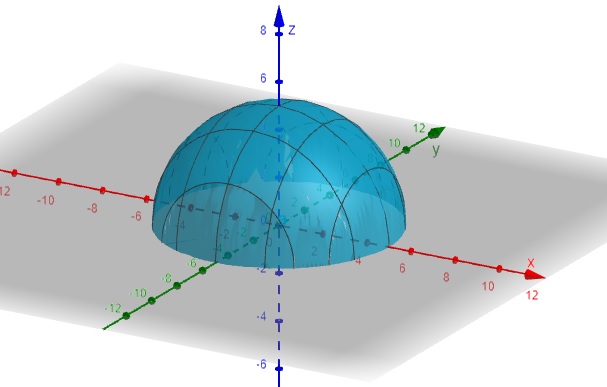
Figura 2.3: Superfície Elipsóide – geogebra.org
d) Outras Superfícies: \[f(x, y) = \frac{1}{\sqrt{x^2-y}}\]
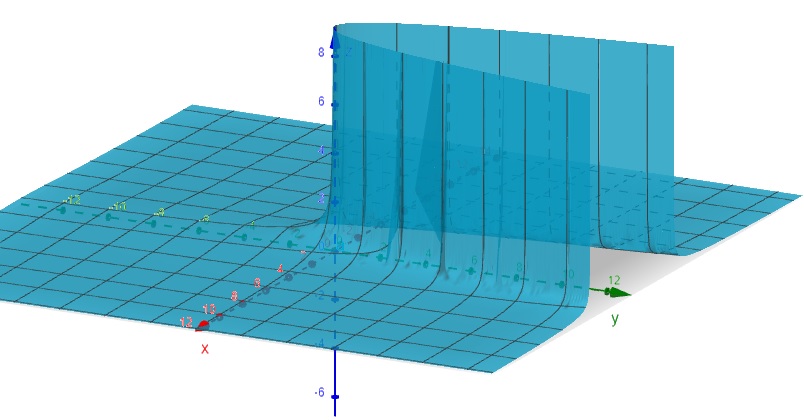
Figura 2.4: Outras Superfícies – geogebra.org
\[f(x, y) = \ln(x^2-y+1)\]
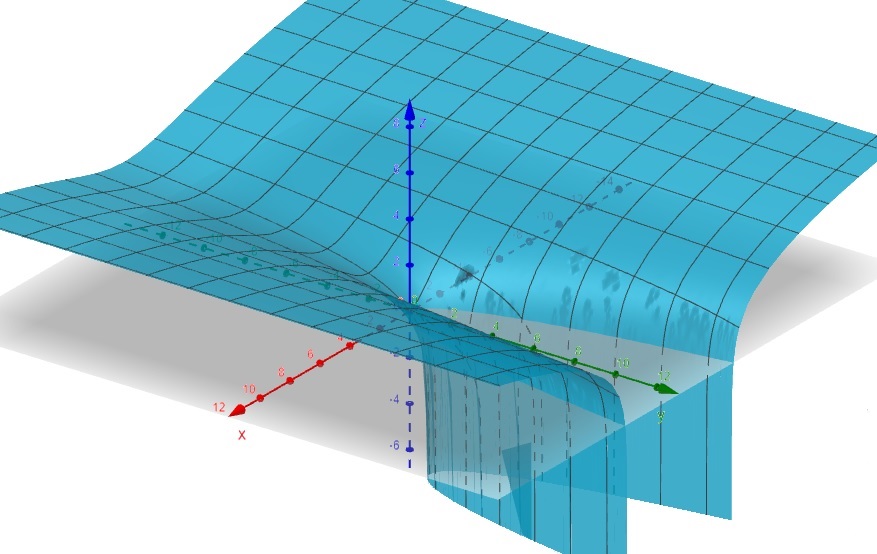
Figura 2.5: Outras Superfícies – geogebra.org
\[f(x, y) = -3xy-\frac{x^4}{4}-\frac{y^4}{4}\]
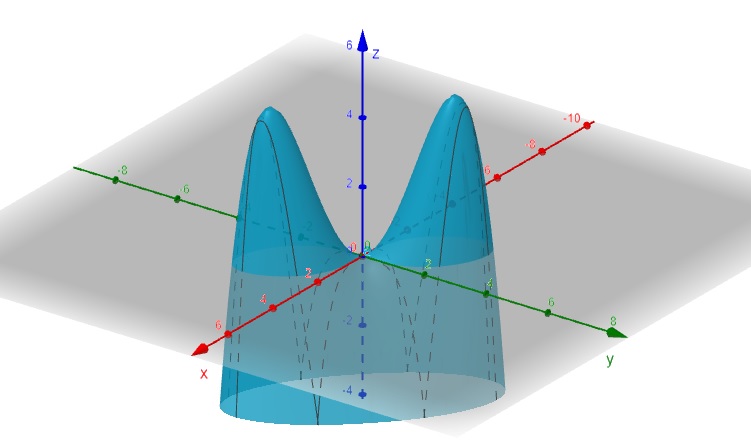
Figura 2.6: Outras Superfícies – geogebra.org
\[f(x, y) = 3\]
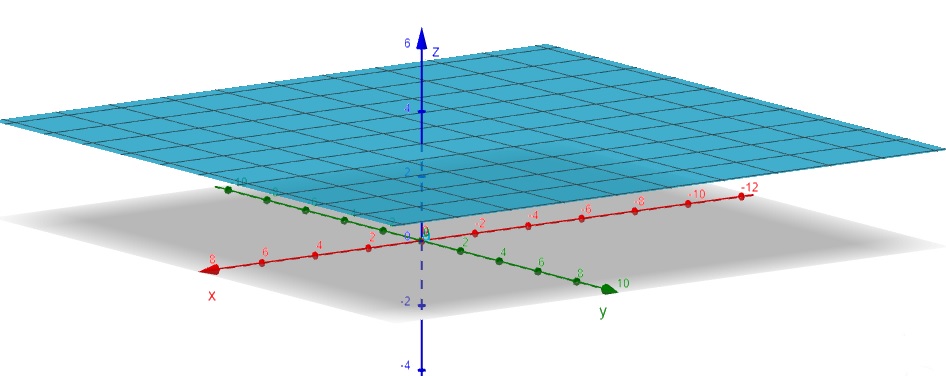
Figura 2.7: Outras Superfícies – geogebra.org
Função de Três ou Mais Variáveis: \[g(x, y, z) = xyz\]
A representação gráfica de funções que dependem de mais de duas variáveis não pode ser facilmente visualizada no espaço tridimensional.
2.4. Aplicações de Funções Multivariadas
Mecânica Clássica: Em mecânica, as leis do movimento de Newton podem ser expressas como funções multivariáveis. Por exemplo, a segunda lei de Newton, \(F = ma\), pode ser considerada uma função do vetor posição \(r(t)\), do tempo \(t\), e da massa \(m\), especialmente quando as forças envolvidas dependem da posição e da velocidade (que é a derivada da posição em relação ao tempo).
Eletromagnetismo: As equações de Maxwell, que descrevem como os campos elétricos e magnéticos interagem com a matéria, são um conjunto de equações diferenciais parciais que naturalmente dependem de funções multivariáveis. Por exemplo, o campo elétrico \(E\) pode ser descrito como uma função do ponto no espaço \((x, y, z)\) e do tempo \(t\), ou seja, \(E(x, y, z, t)\).
Termodinâmica e Mecânica Estatística: A descrição do estado de um sistema termodinâmico muitas vezes envolve variáveis como pressão, volume, temperatura e quantidade de substância, onde, por exemplo, a energia interna do sistema pode ser uma função dessas variáveis, \(U(P, V, T, n)\).
Engenharia Civil e Mecânica: No projeto de estruturas, como pontes ou edifícios, o cálculo de tensões e deformações em materiais sob diferentes cargas envolve funções multivariáveis. A distribuição de tensão em uma viga pode ser modelada como uma função das coordenadas espaciais e das forças aplicadas.
Engenharia Elétrica e Eletrônica: No projeto de circuitos elétricos e sistemas eletrônicos, as leis de Kirchhoff para tensões e correntes são expressas em termos de funções multivariáveis, considerando as tensões em vários pontos do circuito e as correntes que fluem através dos componentes.
Engenharia Química: No projeto e análise de reatores químicos, a taxa de reação e a conversão de reagentes em produtos podem ser funções da concentração dos reagentes, da temperatura, da pressão e do tempo, permitindo a otimização das condições do processo.
Engenharia de Controle: No design de sistemas de controle, modelos matemáticos que descrevem o comportamento dinâmico de sistemas físicos frequentemente dependem de várias variáveis de estado. Por exemplo, o modelo de um avião em voo pode incluir variáveis como velocidade, altitude, ângulo de ataque, entre outras.
2.5. Curvas de Nível
Uma curva de nível de uma função de duas variáveis é um gráfico de uma equação \(f(x,y)=c\), onde c é um valor constante.
As curvas de nível são úteis para visualizar funções de duas variáveis. Em um gráfico tridimensional, elas são curvas no plano \(xy\) ao longo das quais a função tem um valor constante.
Por exemplo, considere as funções: \[f(x,y)=x^2+y^2\].

Figura 2.8: Curva de Nível – geogebra.org
\[f(x,y)=x^2-y^2\].
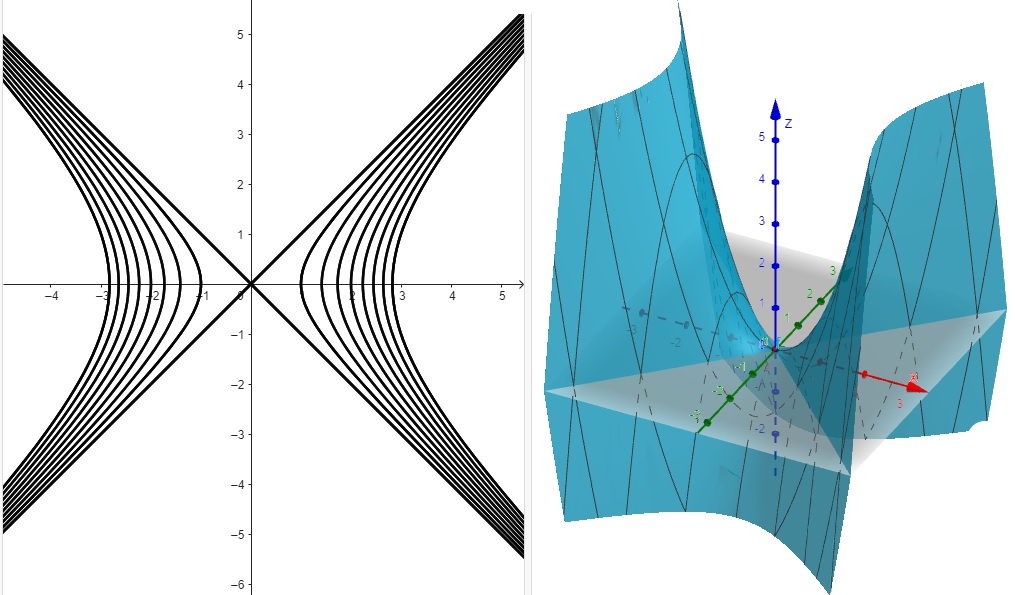
Figura 2.9: Curva de Nível – geogebra.org
\[f(x,y)=3xy-\frac{x^4}{4}-\frac{y^4}{4}\].
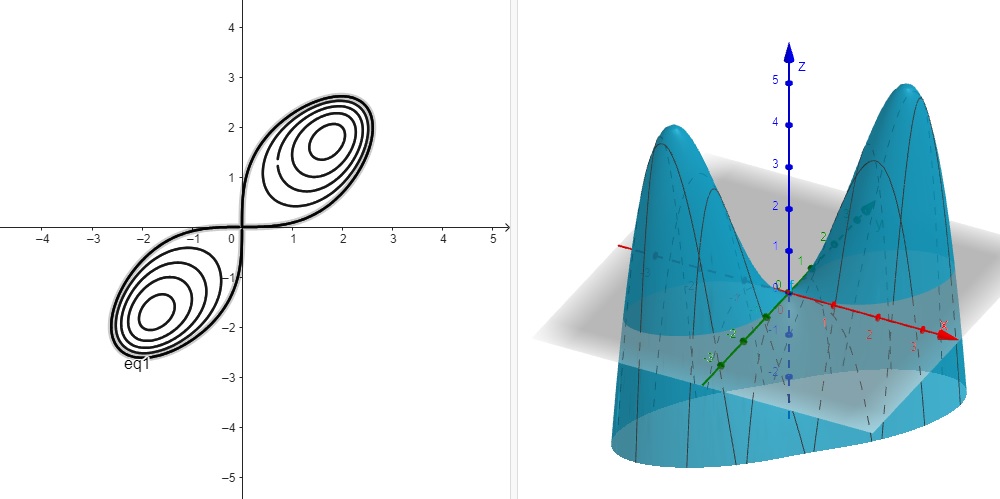
Figura 2.10: Curva de Nível – geogebra.org
2.6. Exercícios
1. Identifique no geogebra as curvas de níveis de algumas funções.
