1. Funções de Uma Variável
Atualizado em: 12 de fevereiro de 2024
Por: Nelson H. Koshoji
1.1. Introdução
Uma função matemática é uma relação entre um conjunto de entradas e um conjunto de saídas permitidas com a propriedade de que cada entrada está relacionada a exatamente uma única saída. Uma maneira intuitiva de pensar sobre funções é considerá-las como máquinas ou processos que tomam entradas (podem ser números, pontos no espaço ou outros objetos matemáticos), realizam alguma operação nessas entradas e, em seguida, produzem saídas.

Figura 1.1: Processos de Entrada e Saída
A definição formal de uma função geralmente é a seguinte: Dados dois conjuntos, A (o domínio) e B (o contradomínio), uma função f de A para B (denotada como: \(f: A \rightarrow B\) é uma regra que atribui a cada elemento \(x\) no domínio A exatamente um elemento \(y\) no contradomínio B. O elemento \(y\) é chamado de imagem de \(x\) sob \(f\), e escrevemos \(y = f(x)\).
As funções são fundamentais na matemática e suas aplicações porque permitem descrever relações entre quantidades, modelar fenômenos e resolver problemas em vários campos da ciência e engenharia. Aqui estão alguns propósitos e usos das funções:
Descrevendo Relações: Funções podem descrever como uma quantidade depende de outra. Por exemplo, a área de um círculo como função de seu raio.
Modelando Fenômenos do Mundo Real: Muitos fenômenos em física, biologia, economia e outros campos podem ser modelados usando funções, permitindo-nos fazer previsões e entender como os sistemas se comportam.
Resolvendo Equações: Funções são usadas na resolução de equações e desigualdades. Ao entender as propriedades de uma função, podemos encontrar suas raízes (valores de \(x\) para os quais \(y = f(x)\)) e analisar seu comportamento.
Analisando Tendências: Em estatísticas e análise de dados, funções ajudam no ajuste de curvas aos dados, ajudando-nos a entender tendências e fazer previsões.
Desenvolvendo Algoritmos: Em ciência da computação, funções são usadas para estruturar programas e realizar cálculos. Elas permitem reutilização de código e programação modular.
Análise Matemática: Funções são centrais para cálculo e análise matemática, onde são usadas para estudar taxas de mudança (derivadas) e acumulação (integrais).
1.2. Principais Tipos de Funções
As funções podem ser categorizadas em vários tipos, com base em suas propriedades específicas e na natureza de seu domínio e imagem. Aqui estão alguns dos principais tipos de funções que você encontrará em matemática:
Funções Lineares
Exemplo:
\[f(x) = 2x + 3\]
Onde \(a = 2\) é a inclinação ou coeficiente angular da reta e \(b = 3\) é o coeficiente linear onde a reta intercepta o eixo \(y\).
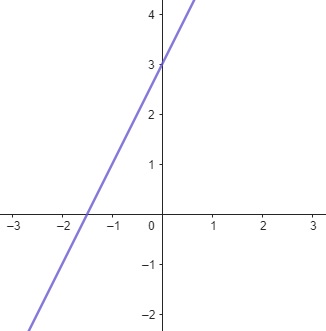
Figura 1.2: Função Linear – App Geogebra.org
Funções Quadráticas
Exemplo:
\[f(x) = x^2 – 4x + 4\]
Onde os coeficientes: \(a = 1\), \(b = -4\) e \(c = 4\).
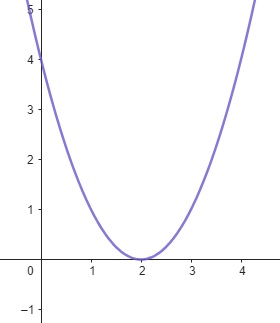
Figura 1.3: Função Quadrática – App Geogebra.org
Funções Polinomiais
São funções que envolvem somas de potências de (x), representadas como \(f(x) = a_nx^n + a_{n-1}x^{n-1}\)\(+ \ldots + a_1x + a_0\), onde \(n\) é um inteiro não negativo, e \(a_n, a_{n-1}, …, a_0\) são constantes. As funções quadráticas são um caso específico de funções polinomiais.
Exemplo:
\[f(x) = x^3 – x^2 + x – 1\]
Esta é uma função polinomial de terceiro grau. Ela tem um comportamento mais complexo do que as lineares ou quadráticas, com pontos de inflexão e extremos locais.
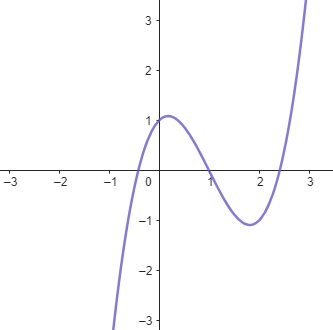
Figura 1.4: Função Polinomial de Grau 3 – App Geogebra.org
Funções Racionais
Uma função racional é a razão de duas funções polinomiais. É da forma \[f(x) = \frac{p(x)}{q(x)}\] onde \(p(x)\) e \(q(x)\) são funções polinomiais, e \(q(x) \neq 0\). Estas funções podem ter assíntotas verticais (valores que \(x\) não pode assumir porque tornariam o denominador zero).
Exemplo:
\[f(x) = \frac{1}{x}\]
Uma função racional simples, onde o numerador é 1 e o denominador é (x). O gráfico tem duas assíntotas: uma vertical em (x = 0) e outra horizontal em (y = 0).
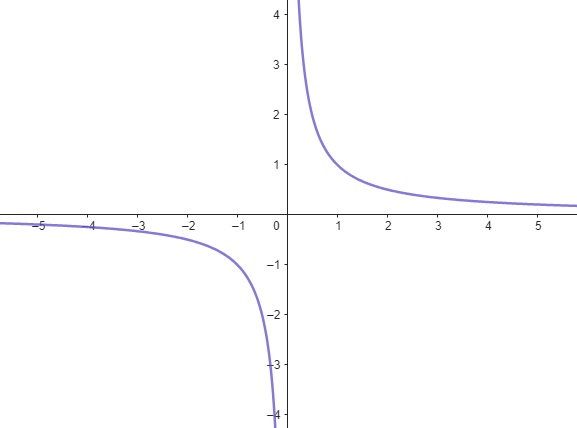
Figura 1.5: Função Racional – App Geogebra.org
Funções Exponenciais
Funções exponenciais têm a forma \(f(x) = a^x\), onde \(a\) é uma constante positiva. Essas funções são usadas para modelar processos de crescimento ou decaimento, como crescimento populacional ou decaimento radioativo.
Exemplo:
\[f(x) = 2^x\]
Esta função exponencial tem uma base de 2. O gráfico mostra um crescimento exponencial, aumentando rapidamente à medida que \(x\) se torna positivo.
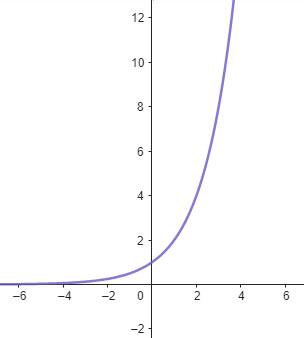
Figura 1.6: Função Exponencial – App Geogebra.org
Funções Logarítmicas
A função logarítmica é a inversa da função exponencial, tipicamente representada como \(f(x) = \log_a(x)\), onde \(a\) é a base do logaritmo. Funções logarítmicas são usadas em medir a intensidade do som, a acidez de uma solução e em muitas outras áreas.
Exemplo:
\[f(x) = \log_2(x)\]
O inverso da função exponencial anterior, com base 2. O gráfico é o reflexo do gráfico da função exponencial correspondente, em relação à linha (y = x).
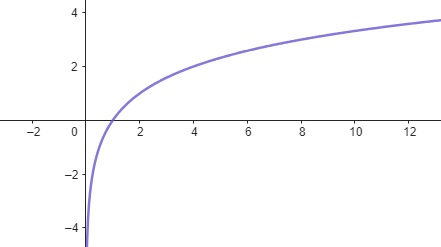
Figura 1.7: Função Logarítmica – App Geogebra.org
Funções Trigonométricas
Estas funções relacionam os ângulos de um triângulo aos comprimentos de seus lados. Funções trigonométricas comuns incluem seno \(\sin(x)\), cosseno \(\cos(x)\), e tangente \(\tan(x)\). Elas são usadas em muitas áreas da ciência e engenharia para modelar fenômenos periódicos.
Exemplo:
\[f(x) = \sin(x)\]
Uma função seno, que modela fenômenos periódicos. O gráfico oscila entre -1 e 1, representando os valores do seno para ângulos de \(x\) (em radianos).
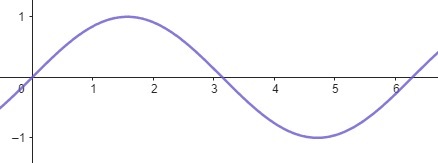
Figura 1.8: Função Seno – App Geogebra.org
Funções Inversas
Se \(f\) é uma função com domínio \(X\) e imagem \(Y\), então sua inversa \(f^{-1}\) é uma função com domínio \(Y\) e imagem \(X\) tal que, se \(f(x) = y\), então \(f^{-1}(y) = x\). Nem todas as funções têm inversas que também são funções.
Exemplo:
Se \(f(x) = x^2\) para \(x \ge 0\), então \(f^{-1}(x) = \sqrt{x}\)
Aqui, a função inversa de \(f(x) = x^2\) (com \(x \ge 0\) para garantir que seja uma função) é \(f^{-1}(x) = \sqrt{x}\), que desfaz a operação de \(f\).
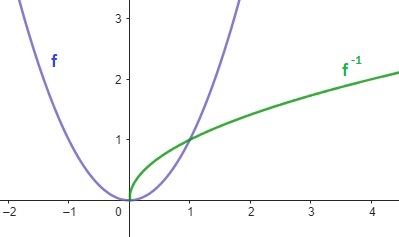
Figura 1.9: Função Inversa – App Geogebra.org
Funções Definidas por Partes
São funções definidas por múltiplas subfunções, cada uma aplicando-se a um certo intervalo do domínio da função principal. Elas podem ser usadas para modelar situações que têm diferentes condições para diferentes intervalos de valores.
Exemplo:
$$
f(x) =
\begin{cases}
x^2 & \text{se } x < 0 \\
x & \text{se } x \ge 0
\end{cases}
$$
Esta função tem uma regra diferente dependendo do valor de \(x\). Para \(x < 0\), ela é quadrática; para \(x \ge 0\), ela é linear.
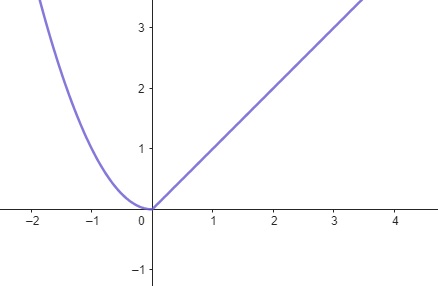
Figura 1.10: Função Definida por Partes – App Geogebra.org
Funções de Valor Absoluto
Estas funções, representadas como \(f(x) = |x|\), retornam o valor absoluto de \(x\).
Exemplo:
\[f(x) = |x|\]
Esta função retorna a magnitude de \(x\) sem considerar seu sinal. O gráfico forma um V, com um ponto de mínimo em \(x = 0\).
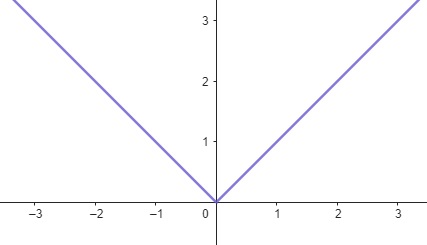
Figura 1.11: Função de Valor Absoluto- App Geogebra.org
1.3. Relação dessas funções com a Física e a Engenharia
As funções matemáticas são fundamentais em vários campos da física e da engenharia, pois oferecem modelos para descrever e analisar fenômenos naturais e sistemas construídos pelo homem. Aqui estão alguns exemplos de como as funções mencionadas são aplicadas nesses campos:
Função Linear: Usada para modelar relações proporcionais diretas, como a lei de Ohm na eletricidade \(V = IR\), onde a tensão \(\textit{V}\) é diretamente proporcional à corrente \(\textit{I}\) através de uma resistência \(\textit{R}\).
Função Quadrática: Em física, é usada para descrever trajetórias de objetos sob a ação da gravidade, como o movimento parabólico de um projétil, onde a altura \(\textit{y}\) varia em função do quadrado do tempo ou da distância horizontal \(\textit{x}\).
Função Polinomial: Usadas para aproximar outras funções ou descrever sistemas que têm múltiplas variáveis e condições. Em engenharia, podem representar a relação entre tensões e deformações em materiais sob diferentes forças.
Função Racional: Aplicações incluem a análise de circuitos em eletrônica, onde a relação entre a tensão de saída e a tensão de entrada pode ser modelada por funções racionais, bem como em dinâmica de fluidos e aerodinâmica.
Função Exponencial: Amplamente usada em decaimento radioativo, crescimento populacional, reações químicas e em finanças para modelar crescimento ou decaimento com o tempo. Em engenharia elétrica, é usada para descrever mudanças de corrente ou tensão em circuitos RC (resistor-capacitor).
Função Logarítmica: Encontra aplicação em escala de intensidade de som (decibéis), na determinação do pH (química), e em escalas logarítmicas usadas para descrever grandezas que variam em ordens de magnitude, como a escala Richter para terremotos.
Função Trigonométrica: Fundamental na descrição de fenômenos periódicos como ondas eletromagnéticas, acústicas, e mecânicas (por exemplo, movimento harmônico simples). Em engenharia, é usada para analisar sistemas oscilatórios, como pontes e edifícios sob a ação do vento.
Função Inversa: Usada em cálculos de engenharia para desfazer efeitos aplicados por funções diretas, por exemplo, em processamento de sinais e na inversão de relações matemáticas para resolver por uma variável desejada.
Função Definida por Partes: Adequada para modelar situações em que diferentes regras se aplicam em diferentes intervalos, como a modelagem de cargas aplicadas em estruturas ou a descrição de sinais em eletrônica digital.
Função de Valor Absoluto: Encontra aplicação em modelagem de distâncias independentemente da direção, como na óptica para representar a diferença de fase entre ondas ou em engenharia para modelar módulos de forças, tensões, e outras grandezas vetoriais.
