Redes Neurais - Multilayer
As redes neurais multicamada (Multilayer Perceptrons – MLPs) são um tipo fundamental de rede neural artificial, que desempenham um papel crucial no campo do aprendizado de máquina e da inteligência artificial. Essas redes são compostas por múltiplas camadas de neurônios, organizadas em uma estrutura de camadas sucessivas, onde cada camada é conectada à próxima. Vamos explorar os conceitos principais que envolvem as redes neurais multicamada de maneira detalhada:
1. Estrutura Básica
Neurônios: Unidades básicas de computação que simulam os neurônios biológicos. Cada neurônio recebe entradas, as processa com base em uma função de ativação e produz uma saída.
Camadas: As MLPs são compostas por três tipos principais de camadas:
- Camada de Entrada: Recebe os dados de entrada para a rede.
- Camadas Ocultas: Camadas intermediárias entre a entrada e a saída, onde ocorre a maior parte do processamento através de pesos e funções de ativação. Uma MLP pode ter uma ou mais camadas ocultas.
- Camada de Saída: Produz a saída final da rede, que é a previsão ou classificação realizada pelo modelo.
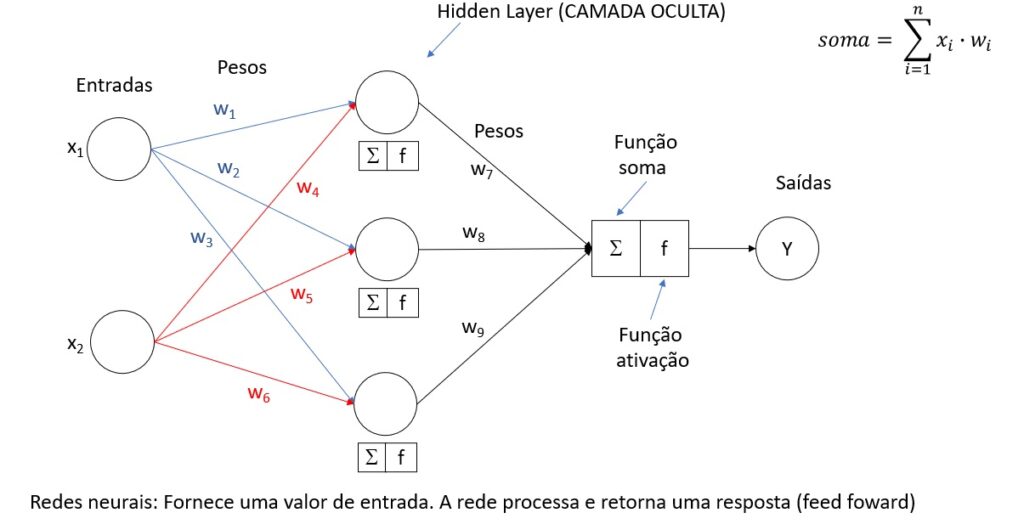
2. Funcionamento
- Propagação para frente (Forward Propagation): O processo começa na camada de entrada, passa pelas camadas ocultas e termina na camada de saída. Em cada neurônio, a soma ponderada das entradas é calculada e passada por uma função de ativação para gerar a saída do neurônio.
- Funções de Ativação: São cruciais para introduzir não-linearidade no modelo, permitindo que a rede aprenda relações complexas. Exemplos incluem a função sigmóide, ReLU (Unidade Linear Retificada) e tanh (Tangente Hiperbólica).
3. Aprendizado
- Retropropagação (Backpropagation): Após a propagação para frente, o erro é calculado na saída. Esse erro é então propagado de volta pela rede, atualizando os pesos dos neurônios de forma a minimizar o erro. Este processo é facilitado por algoritmos de otimização, como o gradiente descendente.
- Atualização dos Pesos: Os pesos são ajustados de acordo com o erro, com o objetivo de reduzir a diferença entre a saída prevista e a real. O tamanho do passo de atualização é determinado pela taxa de aprendizado.
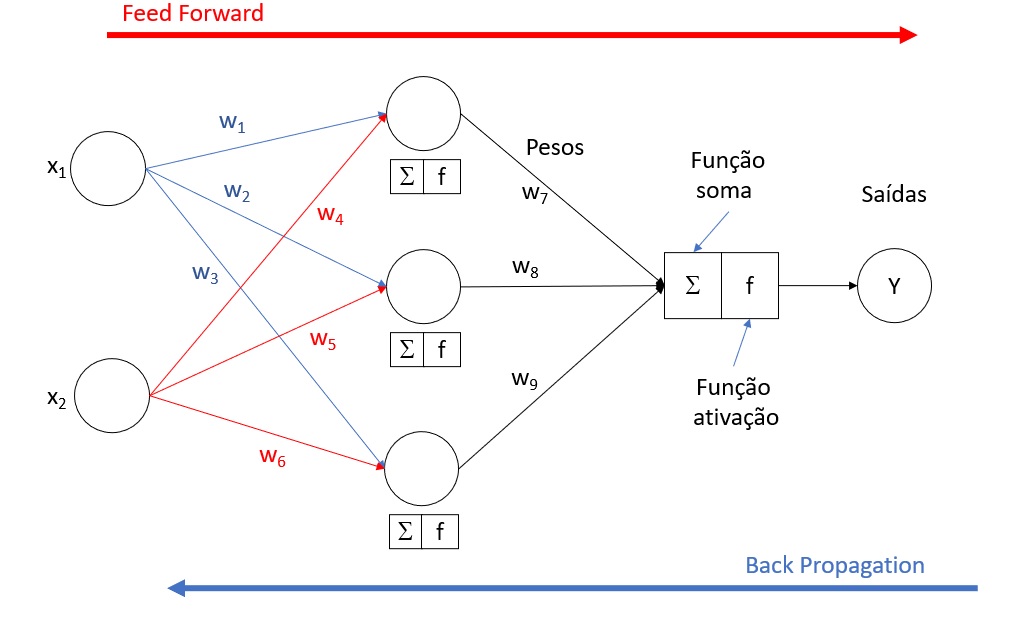
4. Aplicações
As MLPs são versáteis e podem ser aplicadas em uma ampla gama de tarefas, incluindo:
- Classificação e regressão
- Reconhecimento de padrões e imagens
- Previsão de séries temporais
- Sistemas de recomendação
5. Desafios e Considerações
- Overfitting: O modelo pode se tornar muito complexo, memorizando os dados de treinamento em vez de aprender as relações gerais. Técnicas como regularização e dropout são usadas para combater o overfitting.
- Escolha da Arquitetura: Determinar o número de camadas ocultas e o número de neurônios em cada camada é crucial e pode depender muito do problema específico e dos dados disponíveis.
Função de Ativação:
Para as camadas oculta e de saída, você pode usar a função sigmóide, que é comum em redes neurais para classificação binária. A função sigmóide é definida como \(\sigma(x) = \frac{1}{1 + e^{-x}}\), onde \(e\) é a base do logaritmo natural.
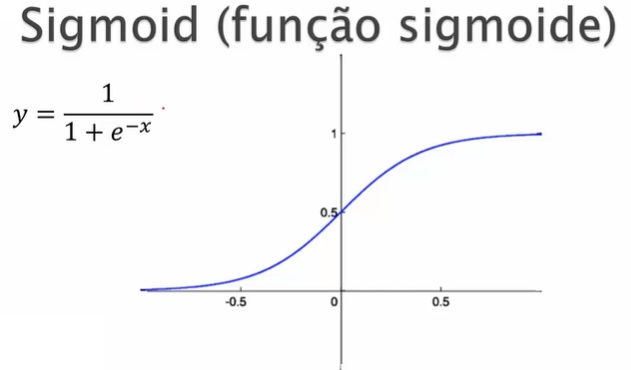
Valores entre 0 e 1 no eixo \(y\)
Se x é um valor alto, ele fica próximo a 1.
Se y é um valor baixo, ele fica próximo a 0.
Não retorna valores negativos
Outras Funções: clique aqui
Operador XOR:
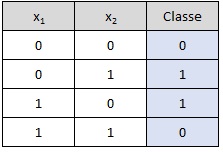
Para implementar uma rede neural que possa resolver o problema XOR, você precisará de uma arquitetura com pelo menos uma camada oculta, além da camada de entrada e saída. Isso é necessário porque o XOR é um problema não linearmente separável, o que significa que não é possível dividir as classes (0 e 1) com uma única linha reta no espaço de entrada. Uma rede com uma camada oculta pode criar fronteiras de decisão não lineares, permitindo resolver problemas como o XOR.
- Entradas:
[[0,0], [0,1], [1,0], [1,1]] - Saídas esperadas:
[[0], [1], [1], [0]] - Pesos da camada de entrada para a camada oculta (
pesos0):np.array([[-0.424, -0.740, -0.961],[0.358, -0.577, -0.469]]) - Pesos da camada oculta para a camada de saída (
pesos1):np.array([[-0.017], [-0.893], [0.148]])
Propagação para Frente (Forward Propagation)
A. Camada de Entrada para Camada Oculta
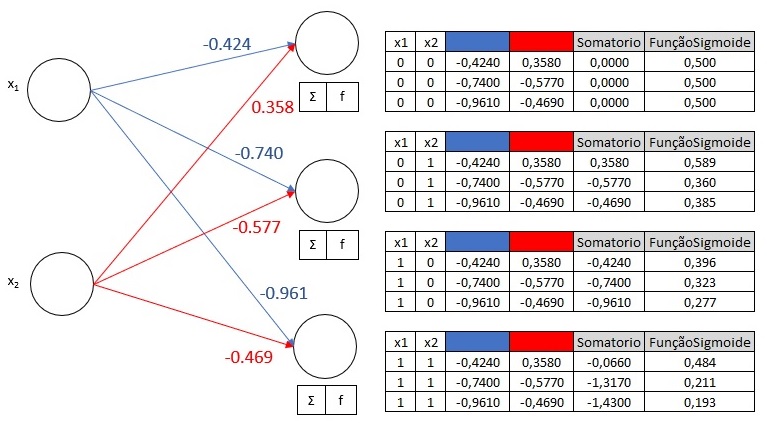
Cálculo da Soma Ponderada na Camada Oculta: Para cada par de entrada, calculamos a soma ponderada das entradas utilizando
pesos0. Isso é feito multiplicando as entradas pelos pesos correspondentes e somando os resultados para cada neurônio na camada oculta.- Aplicação da Função de Ativação Sigmóide: A soma ponderada é passada pela função de ativação sigmóide para cada neurônio na camada oculta. A função sigmóide é dada por \(f(x) = \frac{1}{1 + e^{-x}}\), que mapeia qualquer valor de entrada para um valor entre 0 e 1.
B. Camada Oculta para Camada de Saída
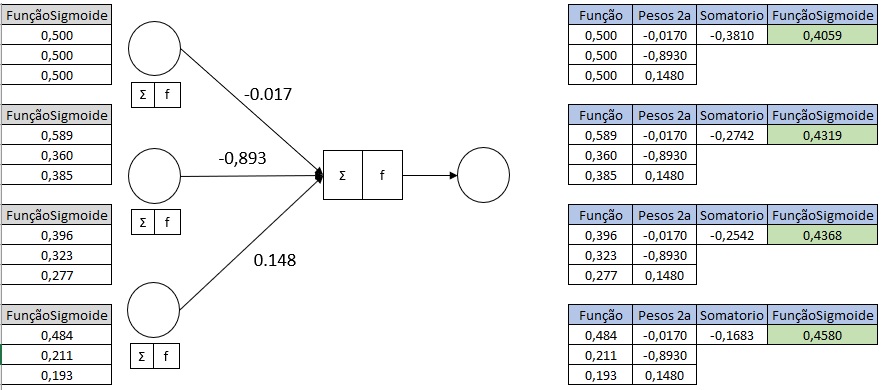
- Cálculo da Soma Ponderada: As saídas da camada oculta, agora transformadas pela função sigmóide, são multiplicadas pelos
pesos1para calcular a soma ponderada na camada de saída. - Aplicação da Função de Ativação Sigmóide: A soma ponderada na camada de saída é novamente passada pela função de ativação sigmóide para obter a saída final da rede para cada entrada.
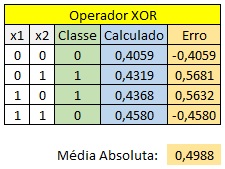
C. Calculo do Erro
- Erro: O erro é calculado como a diferença entre a saída esperada e a saída produzida pela rede.
D. Retropropagação (Backpropagation)
- Durante a retropropagação, os gradientes do erro são calculados em relação a cada peso na rede. Isso envolve a aplicação da regra da cadeia para derivar o gradiente do erro em relação aos pesos entre a camada oculta e a camada de saída (
pesos1) e, em seguida, os pesos entre a camada de entrada e a camada oculta (pesos0). - Função Sigmoide: \(f(x) = \frac{1}{1 + e^{-x}}\)
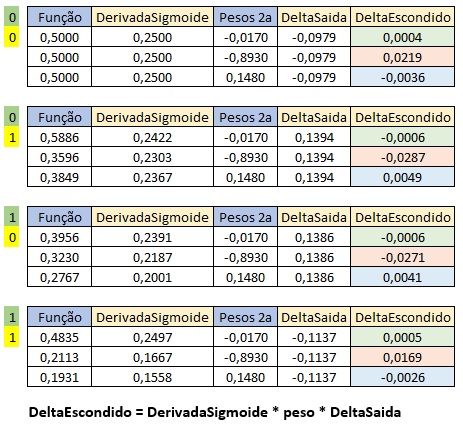
- Derivada Parcial da Função Sigmoide: \(D = y \times (1-y)\)
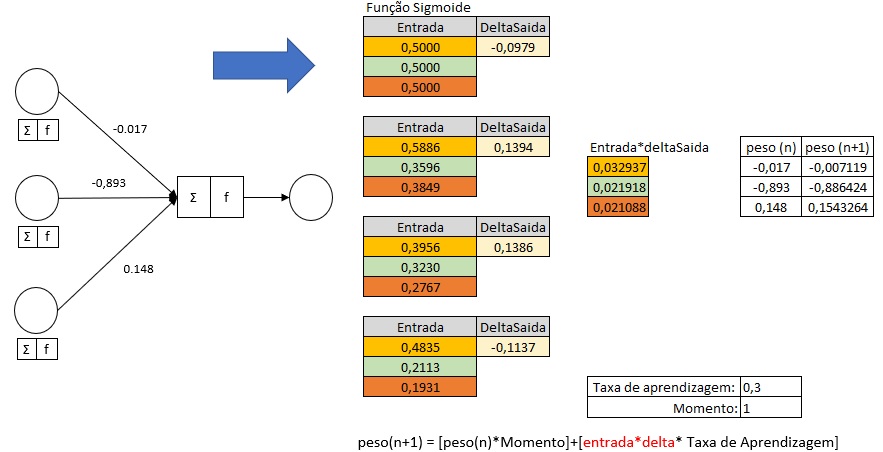
Cálculo do Delta de Saída para calcular o novo peso de peso1:

Cálculo do Delta Escondido para calcular o novo peso de peso0:
Atualização do Peso1:
peso(n+1) = [peso(n)*Momento]+[entrada*delta* Taxa de Aprendizagem]
Taxa de Aprendizagem (learning rate)
- Define quão rápido o algoritmo vai aprender
- Alto: A convergência é rápida mas pode perder o mínimo global
- Baixo: Será mais lento mas tem mais chances de chegar no mínimo global
Momento (momentum)
- Escapar de mínimos locais
- Define o quão confiável é a última alteração
- Alto: aumenta a velocidade da convergência
- Baixo: pode evitar mínimos globais global
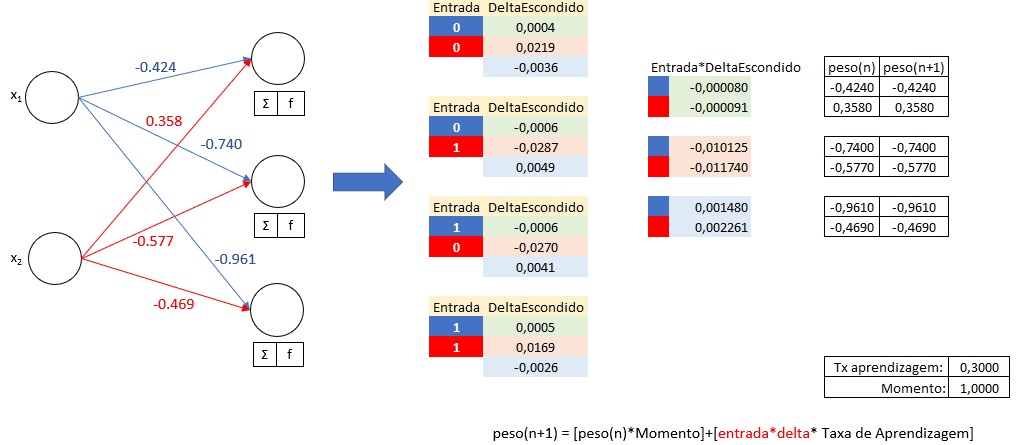
Atualização do Peso0:
Exemplo:
Explicação
- Inicialização: Os pesos são inicializados aleatoriamente.
- Forward Propagation: Calcula a saída da rede neural passando as entradas através das camadas.
- Cálculo do Erro: A diferença entre a saída esperada e a obtida.
- Backpropagation: Ajusta os pesos com base no gradiente do erro.
- Atualização dos Pesos: Os pesos são ajustados em direção à minimização do erro.
Esse exemplo é uma introdução básica à implementação de uma rede neural para o problema XOR. Na prática, frameworks de aprendizado profundo como TensorFlow ou PyTorch fornecem ferramentas muito mais poderosas e flexíveis para construir e treinar redes neurais complexas.
import numpy as np
def sigmoid(soma):
return 1 / (1 + np.exp(-soma))
def sigmoidDerivada(sig):
return sig * (1 - sig)
entradas = np.array([[0,0],[0,1],[1,0],[1,1]])
saidas = np.array([[0],[1],[1],[0]])
pesos0 = 2*np.random.random((2,3)) - 1
pesos1 = 2*np.random.random((3,1)) - 1
# Mostrar os pesos
print("\nPesos da Camada de Entrada:")
print(pesos0)
print("\nPesos da Camada Oculta:")
print(pesos1)
epocas = 10000
taxaAprendizagem = 0.3
momento = 1
for j in range(epocas):
camadaEntrada = entradas
somaSinapse0 = np.dot(camadaEntrada, pesos0)
camadaOculta = sigmoid(somaSinapse0)
somaSinapse1 = np.dot(camadaOculta, pesos1)
camadaSaida = sigmoid(somaSinapse1)
erroCamadaSaida = saidas - camadaSaida
mediaAbsoluta = np.mean(np.abs(erroCamadaSaida))
#print(str(j) + " -> Erro: " + str(mediaAbsoluta))
derivadaSaida = sigmoidDerivada(camadaSaida)
deltaSaida = erroCamadaSaida * derivadaSaida
pesos1Transposta = pesos1.T
deltaSaidaXPeso = deltaSaida.dot(pesos1Transposta)
deltaCamadaOculta = deltaSaidaXPeso * sigmoidDerivada(camadaOculta)
camadaOcultaTransposta = camadaOculta.T
pesosNovo1 = camadaOcultaTransposta.dot(deltaSaida)
pesos1 = (pesos1 * momento) + (pesosNovo1 * taxaAprendizagem)
camadaEntradaTransposta = camadaEntrada.T
pesosNovo0 = camadaEntradaTransposta.dot(deltaCamadaOculta)
pesos0 = (pesos0 * momento) + (pesosNovo0 * taxaAprendizagem)
# Erro final
print("\nErro Final:")
print(str(j) + " -> Erro: " + str(mediaAbsoluta))
# Mostrar os pesos
print("\nPesos da Camada de Entrada:")
print(pesos0)
print("\nPesos da Camada Oculta:")
print(pesos1)
# Teste da rede após treinamento
print("\nSaídas após o treinamento:")
for x in entradas:
camada_oculta = sigmoid(np.dot(x, pesos0))
camada_saida = sigmoid(np.dot(camada_oculta, pesos1))
print(x, "->", camada_saida)
