Produto Escalar
Sejam dois vetores:
\(\vec{u} = x_1\mathbf{i} + y_1\mathbf{j}\)
\(\vec{v} = x_2\mathbf{i} + y_2\mathbf{j}\)
\(\vec{v} \cdot \vec{u} = (x_1 \cdot x_2 + y_1 \cdot y_2) = \alpha\), onde \(\alpha \in R\)
Exemplo:
Calcule o produto escalar entre os vetores:
\(\vec{u} = 5\mathbf{i} +2\mathbf{j}\)
\(\vec{v} = 2\mathbf{i} +4\mathbf{j}\)
\(\vec{v} \cdot \vec{u} = (5 \cdot 2 + 2 \cdot 4) = 18\)
Quando:
\(\vec{u} \cdot \vec{v} = 0\), temos um ângulo reto entre os vetores, ou seja, \(\theta = 90º\)
\(\vec{u} \cdot \vec{v} < 0\), temos um ângulo obtuso entre os vetores, ou seja, \(\theta > 90º\)
\(\vec{u} \cdot \vec{v} > 0\), temos um ângulo agudo entre os vetores, \(\theta < 90º\)
Aplicações:
Cálculo de Ângulos: O ângulo \(\theta\) entre dois vetores \(\vec{v}\) e \(\vec{v}\) pode ser calculado usando a fórmula \(\cos(\theta) = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}|| \vec{v}|}\)
Verificação de Ortogonalidade: Dois vetores são ortogonais (perpendiculares) se seu produto escalar é zero, \(\vec{u} \cdot \vec{v} = 0\)
Exercícios
1. Calcule o produto escalar entre os vetores:
a) \(\vec{u} = (1, 2)\) e \(\vec{v} = (2, -3)\).
Resposta:
b) \(\vec{u} = (1, 2, 3)\) e \(\vec{v} = (4, -5, 6)\).
Resposta: 12
2. Calcule o produto escalar entre \((\vec{u} + \vec{v}) \cdot (2\vec{u} – \vec{v})\):
a) \(\vec{u} = (3, 2, 1)\) e \(\vec{v} = (-1, -4, -1)\).
Resposta: -2
Angulo entre Vetores
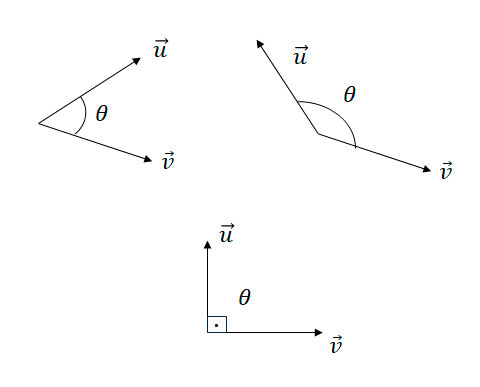
\(\vec{u} \cdot \vec{v} = |\vec{u}||\vec{v}|\cos(\theta)\)
\(\cos(\theta) = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}|| \vec{v}|}\)
\(\theta = \cos^{-1}{(\frac{\vec{u} \cdot \vec{v}}{|\vec{u}|| \vec{v}|})}\)
Exercícios
1. Calcule o ângulo entre os vetores:
a) \(\vec{u} = (5, 2)\) e \(\vec{v} = (2, 4)\)
Resposta: \(41,63º\)
b) \(\vec{u} = (1, 2, 4)\) e \(\vec{v} = (-1, 2, 2)\).
Resposta: \(45º\)
c) \(\vec{u} = (3, 2, 1)\) e \(\vec{v} = (-1, -4,-1)\).
Resposta:
d) Seja os pontos \(A(3,-3,2)\), \(B(2,-1,2)\) e \(C(1,0,2)\)
calcule \(\small \overrightarrow{BA} \cdot \overrightarrow{BC}\)
Resposta: \(150º\)
