Componentes de um vetor
Os componentes de um vetor são elementos fundamentais na descrição de vetores em espaços multidimensionais, como o espaço bidimensional ou tridimensional, entre outros. Esses componentes são essenciais para entender como vetores representam quantidades que têm tanto magnitude quanto direção. Vamos mergulhar nos detalhes desses componentes, sua interpretação e como eles são utilizados para operações vetoriais.
Calcular o componente de um vetor a partir de seu módulo (ou magnitude) envolve um processo que depende do conhecimento de algumas informações adicionais além do módulo do vetor. O módulo de um vetor fornece a “quantidade” ou o tamanho do vetor, mas não sua direção ou orientação no espaço. Para determinar os componentes de um vetor a partir de seu módulo, precisamos conhecer pelo menos a direção do vetor ou o ângulo que ele faz com um dos eixos em um sistema de coordenadas. Vamos explorar como isso pode ser feito em um espaço bidimensional (2D), que pode ser facilmente estendido para dimensões mais altas.

Em relação ao ângulo \(\theta\), temos:
\(x\) é o cateto adjacente ao ângulo \(\theta\)
\(y\) é o cateto oposto ao ângulo \(\theta\)
Logo:
\(\cos(\theta) = \frac{x}{h}\) então: \(x=h.cos(\theta)\)
\(\sin(\theta) = \frac{y}{h}\) então: \(y=h.sin(\theta)\)
Fórmula para as componentes de um vetor:
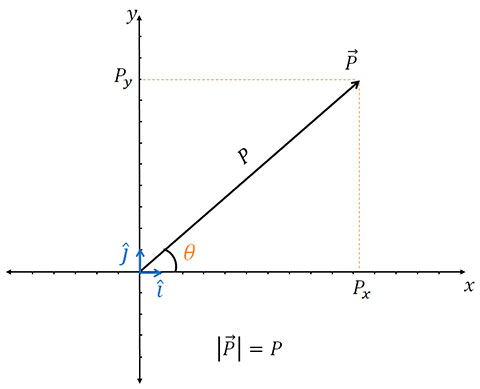
Se:
\(x=h.cos(\theta)\)
\(y=h.sin(\theta)\)
Então:
\(P_x=P.cos(\theta)\)
\(P_y=P.sin(\theta)\)
Logo:
\(\vec{P} = P_x\mathbf{i} + P_x\mathbf{j}\)
Exemplo:
A magnitude do vetor é \(|P| = 8\) e a direção \(\theta = 30º\). Determine as componentes \(P_x\) e \(P_y\) e escreva o vetor \(\vec{P}\).
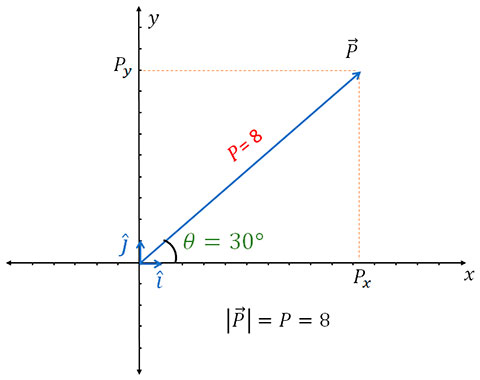
\(P_x = 8 \times \cos(30º)\)
\(P_x = 8 \times 0,8660\)
\(P_x \approx 6,93\)
\(P_y = 8 \times \sin(30º)\)
\(P_y = 8 \times 0,5\)
\(P_y = 4\)
\(\vec{P} = 6,93\mathbf{i} + 4\mathbf{j}\)
Exercícios
1. Suponha que temos um vetor \(\vec{v}\) com um módulo de 5 unidades e que faz um ângulo de 30° com o eixo \(x\). Queremos encontrar os componentes \(v_x\) e \(v_y\).
Resposta: \(\vec{P} = 4,33\mathbf{i} + 2,5\mathbf{j}\)
