Sistema de Coordenadas
Plano \(\mathbb{R}^2\)
O sistema de coordenadas no plano \(\mathbb{R}^2\), também conhecido como sistema de coordenadas cartesianas, é uma forma de determinar a posição de qualquer ponto no plano por meio de dois números, chamados de coordenadas. Esse sistema é fundamental para a geometria analítica, permitindo a representação gráfica de equações algébricas e a análise de formas geométricas e suas propriedades através da álgebra.
O sistema de coordenadas cartesianas em \(\mathbb{R}^2\) é formado por dois eixos perpendiculares entre si, dividindo o plano em quatro regiões denominadas quadrantes. Esses eixos são:
Eixo das Abscissas (Eixo X): Horizontal, utilizado para medir a distância na direção leste-oeste.
Eixo das Ordenadas (Eixo Y): Vertical, utilizado para medir a distância na direção norte-sul.
O ponto de interseção dos dois eixos é chamado de origem, denotado por \(\small O(0, 0)\), e serve como ponto de referência para a localização de todos os outros pontos no plano.
Um ponto no plano \(\mathbb{R}^2\) é representado por um par ordenado \(\small (x, y)\), onde:
\(x\) é a abscissa do ponto, indicando a distância horizontal do ponto à origem, positiva à direita da origem e negativa à esquerda.
\(y\) é a ordenada do ponto, indicando a distância vertical do ponto à origem, positiva acima da origem e negativa abaixo.
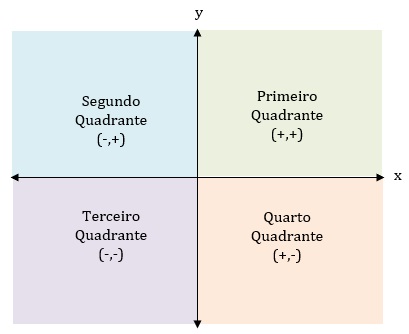
O plano é dividido em quatro quadrantes, numerados em sentido anti-horário:
Primeiro Quadrante: Onde (x > 0) e (y > 0).
Segundo Quadrante: Onde (x < 0) e (y > 0).
Terceiro Quadrante: Onde (x < 0) e (y < 0).
Quarto Quadrante: Onde (x > 0) e (y < 0).
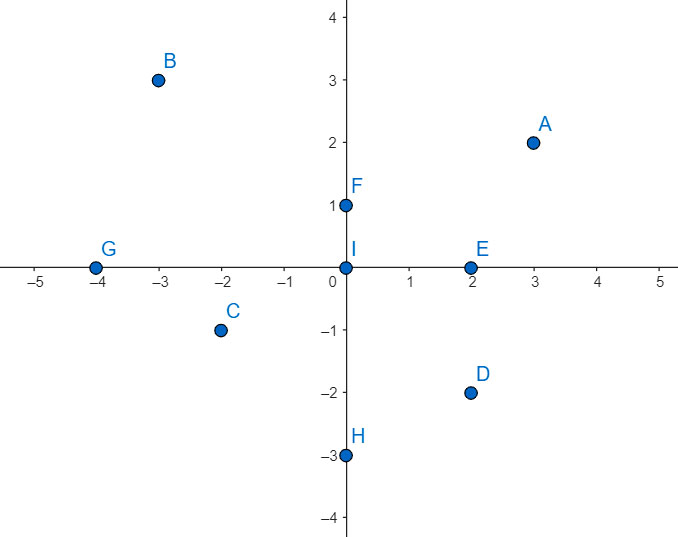
Exemplos
\(\small A=(3,2)\)
\(\small B=(-3,3)\)
\(\small C=(-3,-1)\)
\(\small D=(2,-2)\)
\(\small E=(2,0)\)
\(\small F=(0,1)\)
\(\small G=(-4,0)\)
\(\small H=(0,-3)\)
\(\small I=(0,0)\)
Exercícios
Desenhe em seu caderno, o sistema de coordenadas cartesiana e localize os pontos a seguir:
\(\small A=(4,3)\)
\(\small B=(-5,8)\)
\(\small C=(-4,-3)\)
\(\small D=(6,-2)\)
\(\small E=(9,0)\)
\(\small F=(0,5)\)
\(\small G=(-2,0)\)
\(\small H=(0,-4)\)
\(\small I=(0,0)\)
Plano \(\mathbb{R}^3\)
O sistema de coordenadas no espaço tridimensional, \(\mathbb{R}^3\), expande o conceito do sistema de coordenadas cartesianas do plano \(\mathbb{R}^2\) para um terceiro eixo, permitindo a localização precisa de pontos no espaço tridimensional. Esse sistema é uma ferramenta fundamental em diversas áreas como matemática, física, engenharia, e computação gráfica, pois permite a representação e análise de objetos tridimensionais de forma quantitativa.
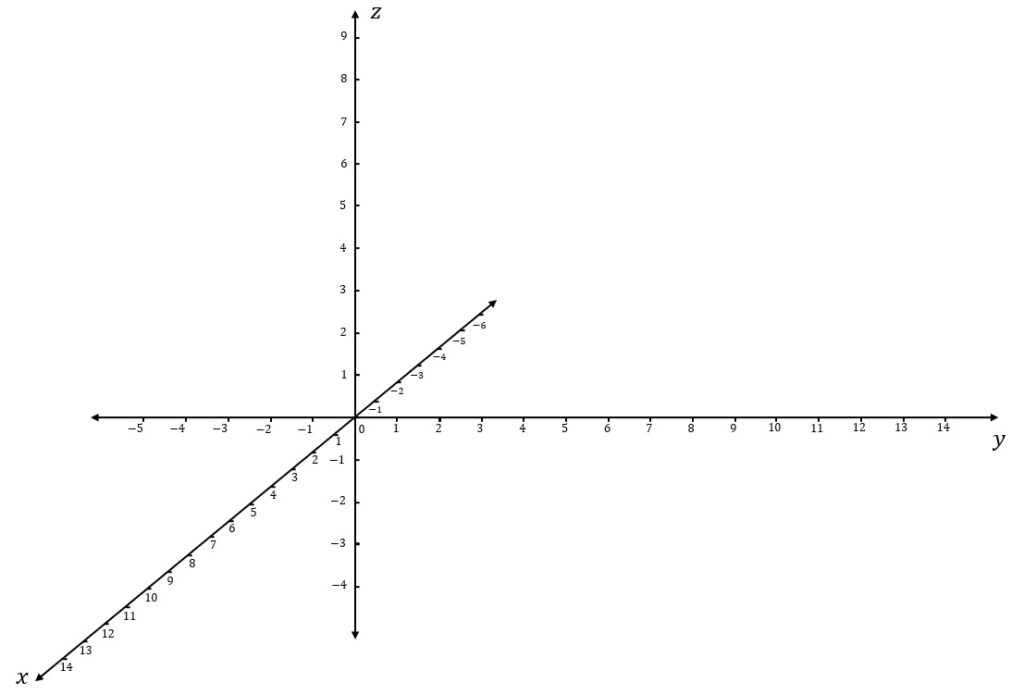
No sistema de coordenadas cartesianas tridimensional, são utilizados três eixos perpendiculares entre si, identificados como:
Eixo X: Representa a dimensão horizontal.
Eixo Y: Representa a dimensão vertical.
Eixo Z: Representa a profundidade, adicionando a terceira dimensão ao sistema.
A interseção dos três eixos ocorre no ponto chamado de origem, denotado por \(\small O(0, 0, 0)\). Esse ponto serve como referência para a localização de todos os outros pontos no espaço tridimensional.
Um ponto no espaço \(\mathbb{R}^3\) é representado por um trio ordenado \(\small (x, y, z)\), onde:
\(x\) é a coordenada no eixo X, indicando a distância horizontal do ponto em relação à origem.
\(y\) é a coordenada no eixo Y, indicando a distância vertical do ponto em relação à origem.
\(z\) é a coordenada no eixo Z, indicando a profundidade do ponto em relação à origem, positiva na direção para fora da origem e negativa na direção para dentro.
Assim como o plano \(\mathbb{R}^2\) é dividido em quadrantes, o espaço \(\mathbb{R}^3\) é dividido em oito regiões denominadas octantes, devido à adição do terceiro eixo. Cada octante é definido pela combinação de sinais das coordenadas \(\small (x, y, z)\), permitindo a classificação de pontos no espaço com base em sua localização relativa à origem.
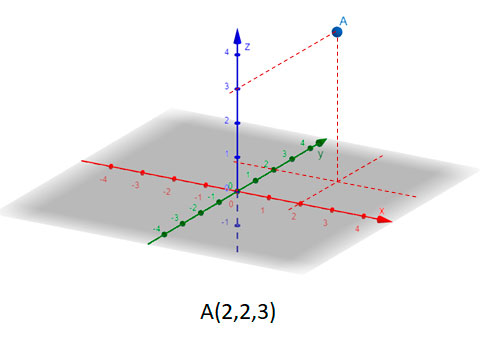
Exemplo
\(\small A=(2,2,3)\)
Exercícios
Desenhe em seu caderno, o sistema de coordenadas cartesiana e localize os pontos a seguir:
\(\small B=(-5,5,4)\)
\(\small C=(-5,-5,4)\)
\(\small D=(5,-5,4)\)
\(\small E=(5,-5,-2)\)
\(\small F=(-5,-5,-1)\)
\(\small G=(-5,5,-1)\)
\(\small H=(5,5,-3)\)
