Grandezas Vetoriais
Grandezas Vetoriais x Grandezas Escalares
Grandezas escalares e grandezas vetoriais são dois tipos fundamentais de quantidades físicas que diferem na forma como são representadas e nas informações que carregam. Ambas são essenciais para descrever fenômenos físicos, mas cada uma possui características e aplicações específicas.
Grandezas Escalares
Uma grandeza escalar é definida como uma quantidade que é completamente descrita por um valor numérico e uma unidade de medida. Escalares não têm direção nem sentido, focando-se apenas na magnitude.
Exemplos:
- Massa: por exemplo, 70 kg
- Temperatura: por exemplo, 25 °C
- Energia: por exemplo, 500 Joules
- Tempo: por exemplo, 20 segundos
- Volume: por exemplo, 2 litros
Escalares são usados quando a direção não é relevante para a descrição do fenômeno em questão.
Grandezas Vetoriais
Uma grandeza vetorial é uma quantidade física que possui tanto magnitude (ou tamanho) quanto direção e sentido. Para representar uma grandeza vetorial, é necessário mais do que um número e uma unidade; também é preciso indicar para onde ela aponta.
Exemplos:
- Velocidade: por exemplo, 60 km/h para o norte
- Força: por exemplo, 10 N para a esquerda
- Aceleração: por exemplo, 2 m/s² para baixo
- Deslocamento: por exemplo, 5 metros para o nordeste
Vetores são frequentemente representados por setas, onde o comprimento da seta indica a magnitude e para onde a seta aponta indica a direção e o sentido da grandeza vetorial.
Direção e Sentido
A diferença mais significativa entre grandezas escalares e vetoriais é que as vetoriais têm direção e sentido, enquanto as escalares não. Isso significa que, ao trabalhar com grandezas vetoriais, é essencial considerar para onde a quantidade está se dirigindo, além de seu tamanho.
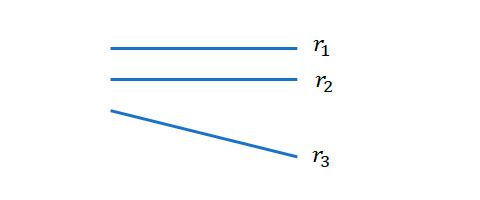
As retas \(r_1\) e \(r_2\) possuem a mesma direção. A reta \(r_3\) possui uma direção diferente de \(r_1\) e \(r_2\).
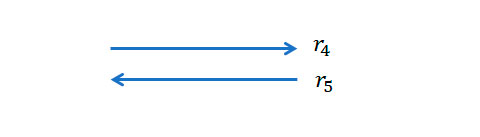
As retas \(r_4\) e \(r_5\) possuem a mesma direção, mas possuem sentidos contrários.
Exemplos
Vamos explorar duas situações distintas para demonstrar a aplicação da soma de forças resultantes, uma envolvendo forças de mesma direção e outra envolvendo forças de direções opostas. Em física, a soma de forças é um conceito fundamental para entender como diferentes forças interagem e afetam o movimento de um objeto.
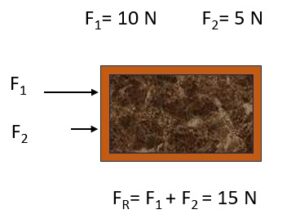
Situação 1: Forças de Mesma Direção
Imagine que temos duas forças atuando sobre um objeto na mesma direção. Por exemplo, Força \(\small F_1 = 10 N\) (Newton) para a direita. Força \(\small F_2 = 5 N\) (Newton) também para a direita. Para encontrar a força resultante \(\small F_R\) que atua sobre o objeto, simplesmente somamos as magnitudes das forças, já que elas estão na mesma direção:
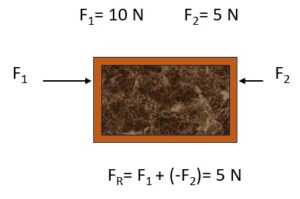
Situação 2: Forças de Direções Opostas
Agora, consideremos o caso em que temos duas forças atuando sobre o mesmo objeto, mas em direções opostas. Por exemplo, Força \(F_1 = 10 N\) (Newton) para a direita. Força \(F_2 = 5 N\) (Newton) para a esquerda. Para encontrar a força resultante \(F_R\) que atua sobre o objeto, simplesmente subtraímos as magnitudes das forças, devido a força contrária: