6. Vetor Gradiente
Atualizado em: 25 de fevereiro de 2024
Por: Nelson H. Koshoji
6.1. Vetor Gradiente
O vetor gradiente é um conceito fundamental no cálculo multivariável e na análise vetorial, representando um vetor que aponta na direção de maior taxa de aumento de uma função escalar. Formalmente, para uma função \(f(x_1, x_2, …, x_n)\) de várias variáveis, o vetor gradiente de (f) é denotado por \(\nabla f\) ou \(\text{grad} f\) e é definido como o vetor das derivadas parciais de (f):
\[\nabla f = (\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2}, …, \frac{\partial f}{\partial x_n})\]
Para que serve o Vetor Gradiente:
-
Direção de Maior Crescimento: O vetor gradiente aponta na direção de maior aumento da função no ponto considerado. Isso significa que, se você se mover na direção do vetor gradiente a partir de um ponto dado, você estará seguindo o caminho de maior inclinação ascendente.
-
Otimização de Funções: Em problemas de otimização, o vetor gradiente é utilizado para encontrar os pontos de máximo e mínimo locais de uma função. Métodos como o gradiente descendente utilizam o vetor gradiente para minimizar uma função, ajustando iterativamente os parâmetros na direção oposta ao gradiente.
-
Análise de Topologia de Superfícies: O vetor gradiente pode ser usado para entender a topologia e as características de superfícies definidas por funções escalares, como a determinação de pontos críticos (onde o gradiente é zero) e a análise da concavidade ou convexidade em tais pontos.
-
Fluxo e Campo de Direções: Em física e engenharia, o vetor gradiente é fundamental para descrever o fluxo de campos, como o campo elétrico (que pode ser descrito como o gradiente negativo do potencial elétrico) ou o fluxo de calor (direção e magnitude do fluxo térmico).
-
Métodos Numéricos e Algoritmos de Aprendizado de Máquina: O vetor gradiente desempenha um papel crucial em algoritmos de aprendizado de máquina, especialmente em técnicas de otimização como a descida do gradiente, usada para ajustar os parâmetros de modelos de machine learning para minimizar uma função de custo.
6.2. Interpretação Geométrica
Seja a função \(f(x,y) = -x^2-y^2+9\)
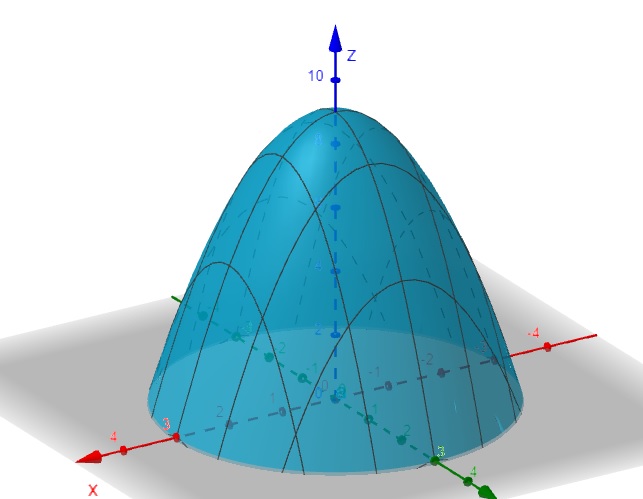
\[\nabla f(x,y) = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\]
\[\frac{\partial f}{\partial x} = -2x\]
\[\frac{\partial f}{\partial x} = -2y\]
\[\nabla f(x,y) = (-2x, -2y)\]
no ponto A(1,2,4):
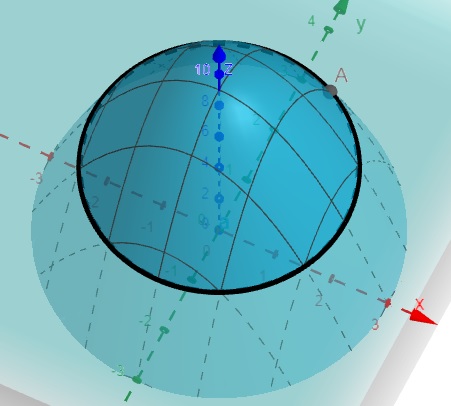
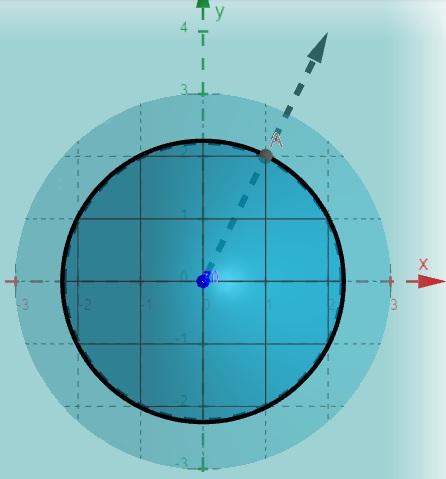
O vetor gradiente nos diz em que direção a função cresce mais rápido, partindo do ponto (x_0,y_0), nesse caso (1,2)
\[\nabla f(1,2) = (-2, -4)\]
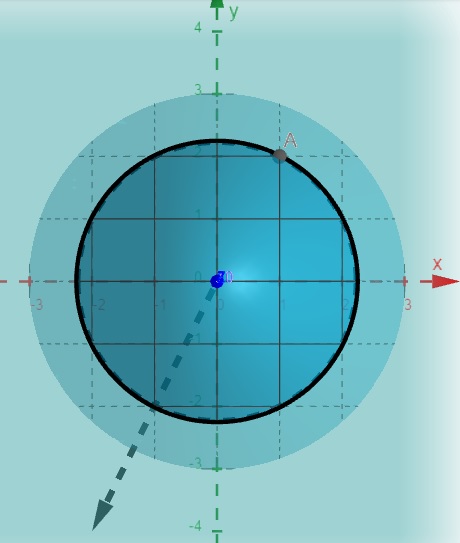
O vetor gradiente oposto nos diz em que direção a função decresce mais rápido, partindo do ponto (x_0,y_0), nesse caso (1,2)
\[-\nabla f(1,2) = (2, 4)\]
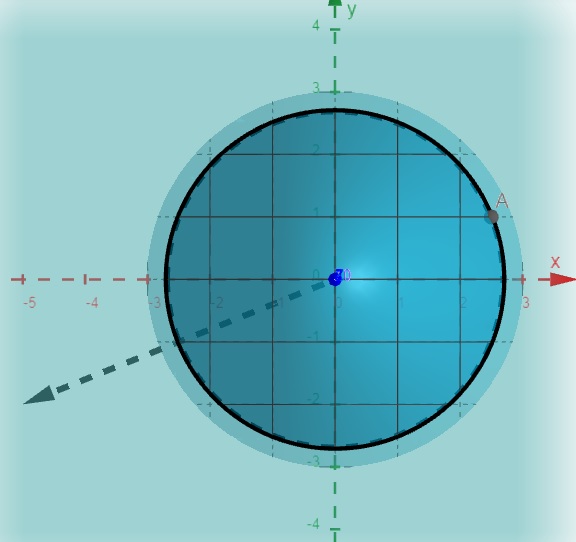
Agora é sua vez encontre o vetor gradiente, em que direção a função cresce mais rápido, partindo do ponto (3,1)
- Encontre o Ponto
- calcule o vetor Gradiente:
no ponto A(2.5,1,1.75):
\[\nabla f(2.5,1) = (-5, -2)\]
Exercício
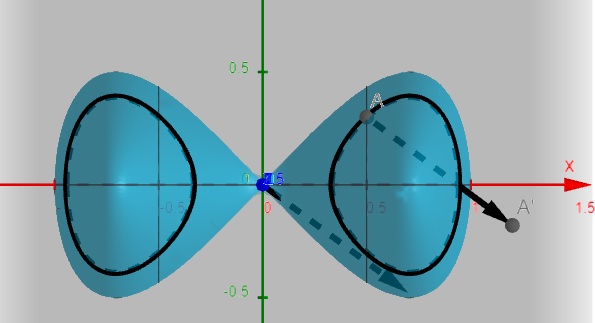
Seja a função \(f(x,y) = -4x^4+4x^2-4y^2\)
Entre o vetor gradiente dessa função no ponto (0.5,0.3)
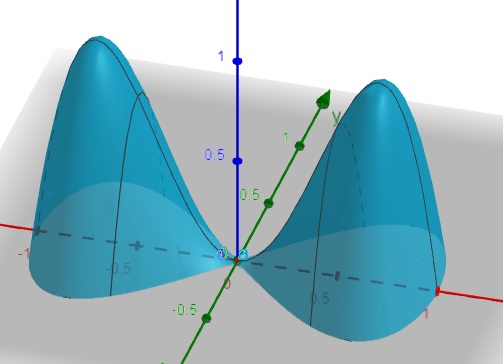
Ponto (0.5,0.3,0.39)