5. Máximos, Mínimos e Ponto de Sela
Atualizado em: 25 de fevereiro de 2024
Por: Nelson H. Koshoji
5.1. Pontos Críticos:
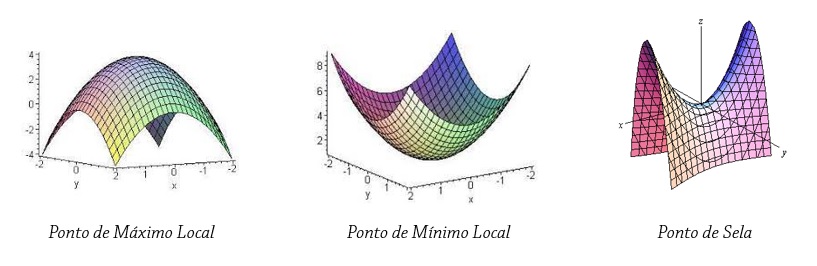
5.2. Como encontrar
Seja \(u = f(x,y)\), o ponto \(P(x_o,y_o,z_o)\) é chamado de crítico se:
\[\large\frac{\partial u}{\partial x} = 0\]
\[\large\frac{\partial u}{\partial y} = 0\]
Como encontrar:
1. Encontrar as derivadas parciais de 1a e 2a ordem da função: \(u=f(x,y)\):
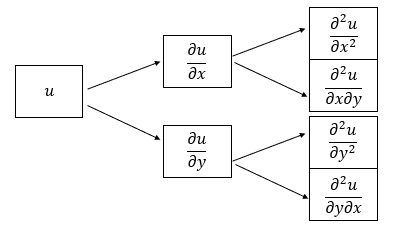
2. Igualar as derivadas parciais de 1a ordem à zero e encontrar o ponto crítico \(P(x_o,y_o,z_o)\):

3. Montar um determinante, chamado de Hessiano, com as derivadas parciais de 2a ordem para classificar os pontos críticos:
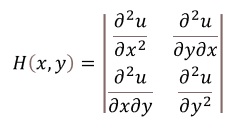
Se o determinante:
\(H=0\) – (Nada podemos concluir)
\(H<0\) – (\(u=f(x,y)\) tem ponto de sela no ponto crítico \(P(x_0,y_0,z_0)\))
\(H>0\) e \(\frac{\partial^2 u}{\partial x^2} > 0\) – (\(u=f(x,y)\) tem ponto de mínimo local no ponto crítico \(P(x_0,y_0,z_0)\))
\(H>0\) e \(\frac{\partial^2 u}{\partial x^2} < 0\) – (\(u=f(x,y)\) tem ponto de máximo local no ponto crítico \(P(x_0,y_0,z_0)\))
5.3. Exercícios
1. Determine os pontos críticos da função, se existir:
\(f(x,y)=x^2+y^2-4x+5\)
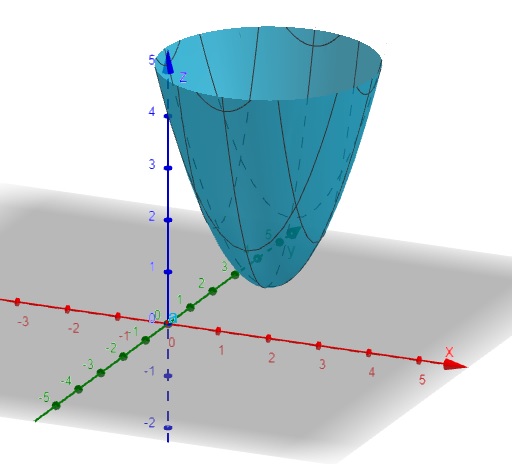
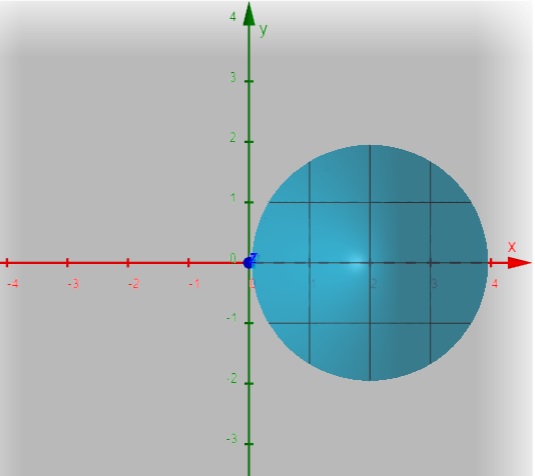
2. Determine os pontos críticos da função, se existir:
\(f(x,y)=3x^2+y^2-2xy+2y\)